Continuous Mean-Zero Disagreement-Regularized Imitation Learning (CMZ-DRIL)

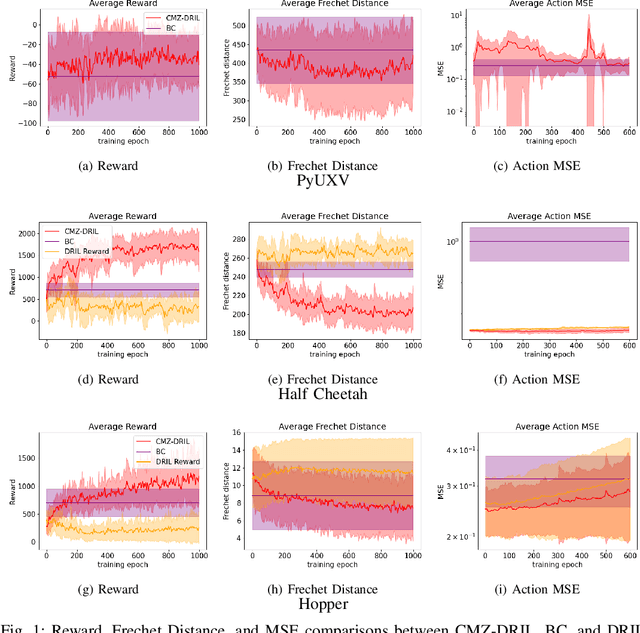
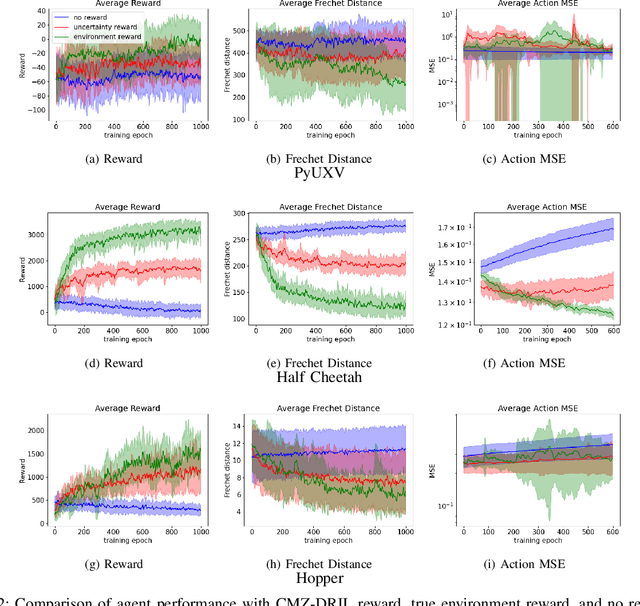
Machine-learning paradigms such as imitation learning and reinforcement learning can generate highly performant agents in a variety of complex environments. However, commonly used methods require large quantities of data and/or a known reward function. This paper presents a method called Continuous Mean-Zero Disagreement-Regularized Imitation Learning (CMZ-DRIL) that employs a novel reward structure to improve the performance of imitation-learning agents that have access to only a handful of expert demonstrations. CMZ-DRIL uses reinforcement learning to minimize uncertainty among an ensemble of agents trained to model the expert demonstrations. This method does not use any environment-specific rewards, but creates a continuous and mean-zero reward function from the action disagreement of the agent ensemble. As demonstrated in a waypoint-navigation environment and in two MuJoCo environments, CMZ-DRIL can generate performant agents that behave more similarly to the expert than primary previous approaches in several key metrics.

A Risk-Sensitive Approach to Policy Optimization

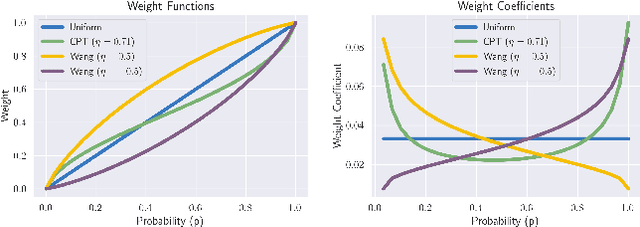
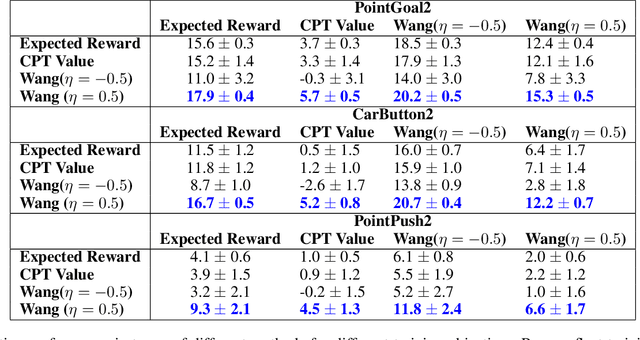
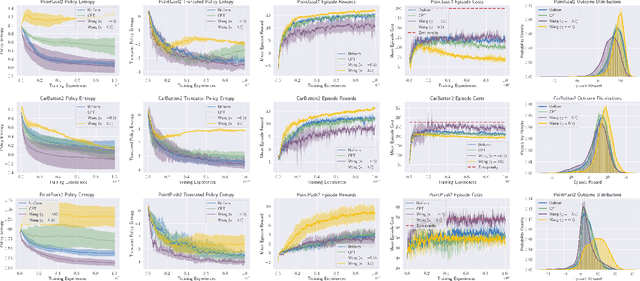
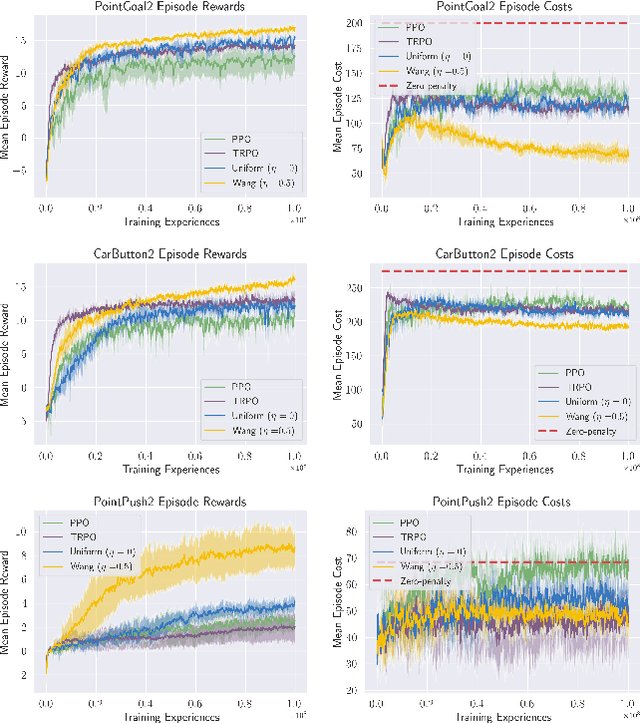
Standard deep reinforcement learning (DRL) aims to maximize expected reward, considering collected experiences equally in formulating a policy. This differs from human decision-making, where gains and losses are valued differently and outlying outcomes are given increased consideration. It also fails to capitalize on opportunities to improve safety and/or performance through the incorporation of distributional context. Several approaches to distributional DRL have been investigated, with one popular strategy being to evaluate the projected distribution of returns for possible actions. We propose a more direct approach whereby risk-sensitive objectives, specified in terms of the cumulative distribution function (CDF) of the distribution of full-episode rewards, are optimized. This approach allows for outcomes to be weighed based on relative quality, can be used for both continuous and discrete action spaces, and may naturally be applied in both constrained and unconstrained settings. We show how to compute an asymptotically consistent estimate of the policy gradient for a broad class of risk-sensitive objectives via sampling, subsequently incorporating variance reduction and regularization measures to facilitate effective on-policy learning. We then demonstrate that the use of moderately "pessimistic" risk profiles, which emphasize scenarios where the agent performs poorly, leads to enhanced exploration and a continual focus on addressing deficiencies. We test the approach using different risk profiles in six OpenAI Safety Gym environments, comparing to state of the art on-policy methods. Without cost constraints, we find that pessimistic risk profiles can be used to reduce cost while improving total reward accumulation. With cost constraints, they are seen to provide higher positive rewards than risk-neutral approaches at the prescribed allowable cost.

On the Complexity of Reconnaissance Blind Chess

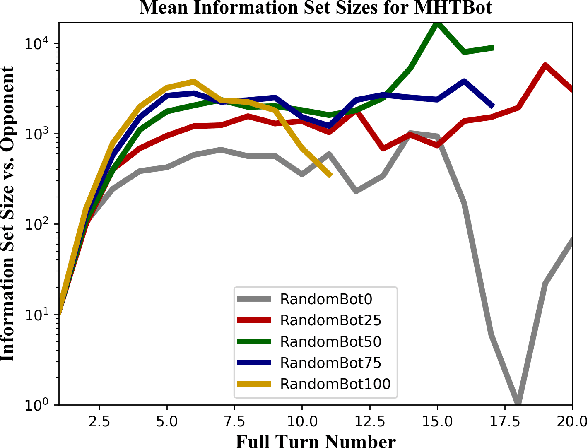
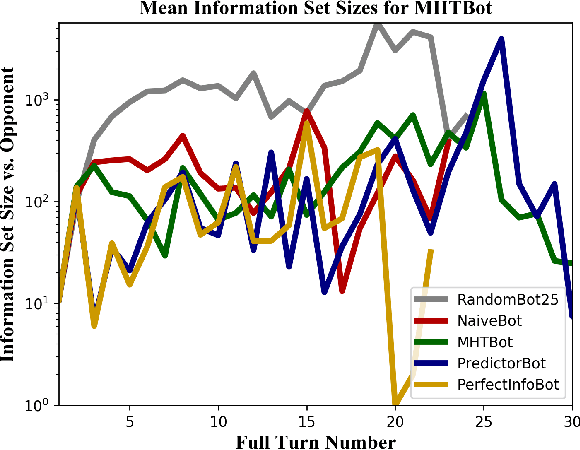
This paper provides a complexity analysis for the game of reconnaissance blind chess (RBC), a recently-introduced variant of chess where each player does not know the positions of the opponent's pieces a priori but may reveal a subset of them through chosen, private sensing actions. In contrast to commonly studied imperfect information games like poker and Kriegspiel, an RBC player does not know what the opponent knows or has chosen to learn, exponentially expanding the size of the game's information sets (i.e., the number of possible game states that are consistent with what a player has observed). Effective RBC sensing and moving strategies must account for the uncertainty of both players, an essential element of many real-world decision-making problems. Here we evaluate RBC from a game theoretic perspective, tracking the proliferation of information sets from the perspective of selected canonical bot players in tournament play. We show that, even for effective sensing strategies, the game sizes of RBC compare to those of Go while the average size of a player's information set throughout an RBC game is much greater than that of a player in Heads-up Limit Hold 'Em. We compare these measures of complexity among different playing algorithms and provide cursory assessments of the various sensing and moving strategies.