Ruian Shi
Structured Neural Networks for Density Estimation and Causal Inference
Nov 03, 2023



Abstract:Injecting structure into neural networks enables learning functions that satisfy invariances with respect to subsets of inputs. For instance, when learning generative models using neural networks, it is advantageous to encode the conditional independence structure of observed variables, often in the form of Bayesian networks. We propose the Structured Neural Network (StrNN), which injects structure through masking pathways in a neural network. The masks are designed via a novel relationship we explore between neural network architectures and binary matrix factorization, to ensure that the desired independencies are respected. We devise and study practical algorithms for this otherwise NP-hard design problem based on novel objectives that control the model architecture. We demonstrate the utility of StrNN in three applications: (1) binary and Gaussian density estimation with StrNN, (2) real-valued density estimation with Structured Autoregressive Flows (StrAFs) and Structured Continuous Normalizing Flows (StrCNF), and (3) interventional and counterfactual analysis with StrAFs for causal inference. Our work opens up new avenues for learning neural networks that enable data-efficient generative modeling and the use of normalizing flows for causal effect estimation.
Splicing Up Your Predictions with RNA Contrastive Learning
Oct 17, 2023Abstract:In the face of rapidly accumulating genomic data, our understanding of the RNA regulatory code remains incomplete. Recent self-supervised methods in other domains have demonstrated the ability to learn rules underlying the data-generating process such as sentence structure in language. Inspired by this, we extend contrastive learning techniques to genomic data by utilizing functional similarities between sequences generated through alternative splicing and gene duplication. Our novel dataset and contrastive objective enable the learning of generalized RNA isoform representations. We validate their utility on downstream tasks such as RNA half-life and mean ribosome load prediction. Our pre-training strategy yields competitive results using linear probing on both tasks, along with up to a two-fold increase in Pearson correlation in low-data conditions. Importantly, our exploration of the learned latent space reveals that our contrastive objective yields semantically meaningful representations, underscoring its potential as a valuable initialization technique for RNA property prediction.
Segmenting Hybrid Trajectories using Latent ODEs
May 09, 2021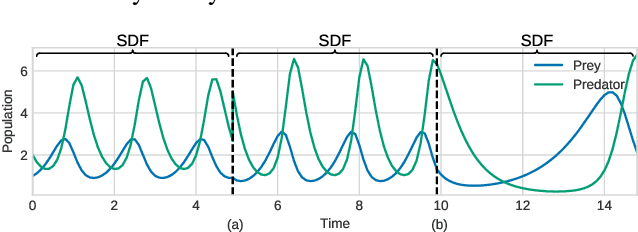
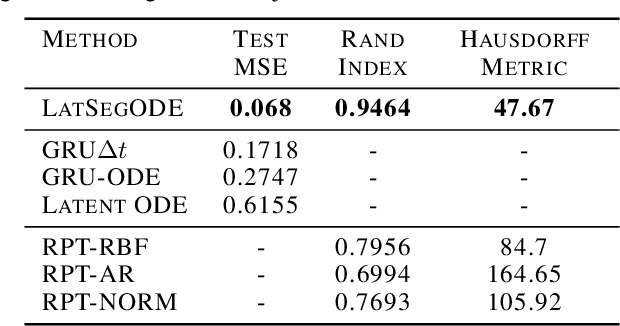
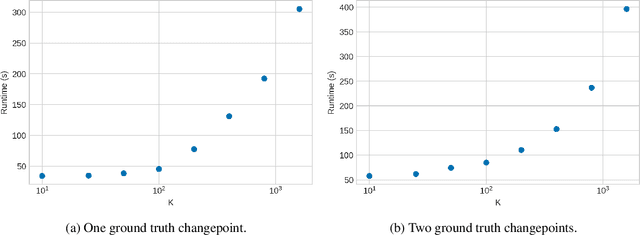
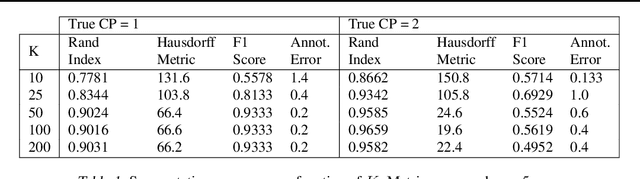
Abstract:Smooth dynamics interrupted by discontinuities are known as hybrid systems and arise commonly in nature. Latent ODEs allow for powerful representation of irregularly sampled time series but are not designed to capture trajectories arising from hybrid systems. Here, we propose the Latent Segmented ODE (LatSegODE), which uses Latent ODEs to perform reconstruction and changepoint detection within hybrid trajectories featuring jump discontinuities and switching dynamical modes. Where it is possible to train a Latent ODE on the smooth dynamical flows between discontinuities, we apply the pruned exact linear time (PELT) algorithm to detect changepoints where latent dynamics restart, thereby maximizing the joint probability of a piece-wise continuous latent dynamical representation. We propose usage of the marginal likelihood as a score function for PELT, circumventing the need for model complexity-based penalization. The LatSegODE outperforms baselines in reconstructive and segmentation tasks including synthetic data sets of sine waves, Lotka Volterra dynamics, and UCI Character Trajectories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge