Active Measure Reinforcement Learning for Observation Cost Minimization

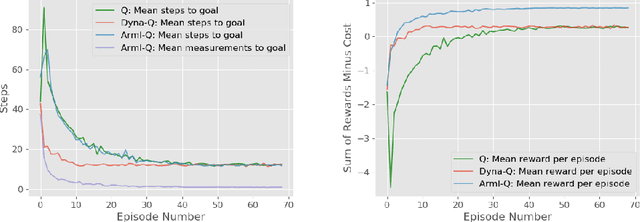
Standard reinforcement learning (RL) algorithms assume that the observation of the next state comes instantaneously and at no cost. In a wide variety of sequential decision making tasks ranging from medical treatment to scientific discovery, however, multiple classes of state observations are possible, each of which has an associated cost. We propose the active measure RL framework (Amrl) as an initial solution to this problem where the agent learns to maximize the costed return, which we define as the discounted sum of rewards minus the sum of observation costs. Our empirical evaluation demonstrates that Amrl-Q agents are able to learn a policy and state estimator in parallel during online training. During training the agent naturally shifts from its reliance on costly measurements of the environment to its state estimator in order to increase its reward. It does this without harm to the learned policy. Our results show that the Amrl-Q agent learns at a rate similar to standard Q-learning and Dyna-Q. Critically, by utilizing an active strategy, Amrl-Q achieves a higher costed return.

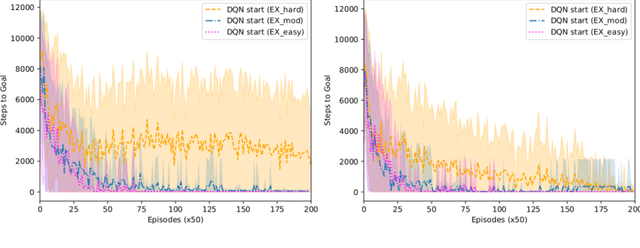
Reinforcement Learning in a Physics-Inspired Semi-Markov Environment

Reinforcement learning (RL) has been demonstrated to have great potential in many applications of scientific discovery and design. Recent work includes, for example, the design of new structures and compositions of molecules for therapeutic drugs. Much of the existing work related to the application of RL to scientific domains, however, assumes that the available state representation obeys the Markov property. For reasons associated with time, cost, sensor accuracy, and gaps in scientific knowledge, many scientific design and discovery problems do not satisfy the Markov property. Thus, something other than a Markov decision process (MDP) should be used to plan / find the optimal policy. In this paper, we present a physics-inspired semi-Markov RL environment, namely the phase change environment. In addition, we evaluate the performance of value-based RL algorithms for both MDPs and partially observable MDPs (POMDPs) on the proposed environment. Our results demonstrate deep recurrent Q-networks (DRQN) significantly outperform deep Q-networks (DQN), and that DRQNs benefit from training with hindsight experience replay. Implications for the use of semi-Markovian RL and POMDPs for scientific laboratories are also discussed.

Optimizing thermodynamic trajectories using evolutionary reinforcement learning

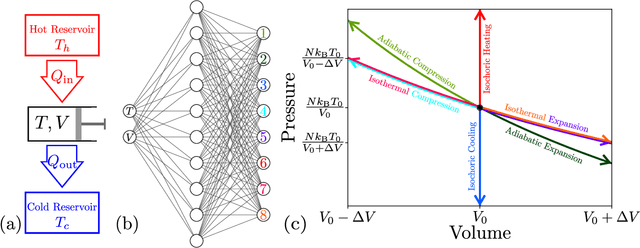
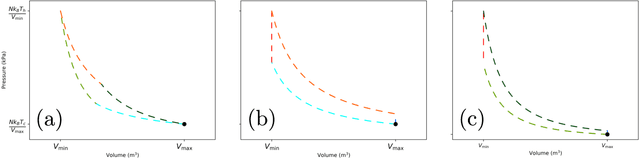
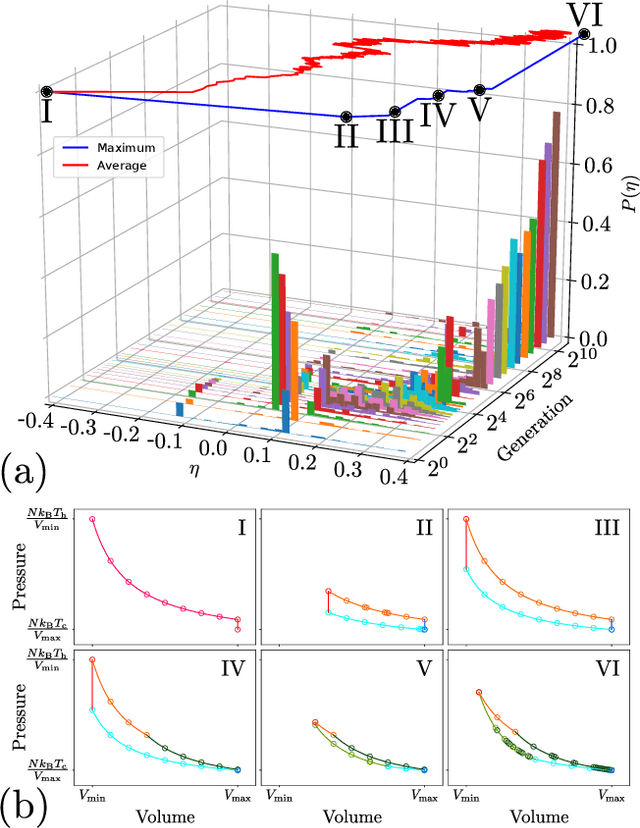
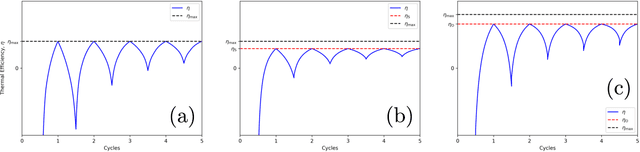
Using a model heat engine we show that neural network-based reinforcement learning can identify thermodynamic trajectories of maximal efficiency. We use an evolutionary learning algorithm to evolve a population of neural networks, subject to a directive to maximize the efficiency of a trajectory composed of a set of elementary thermodynamic processes; the resulting networks learn to carry out the maximally-efficient Carnot, Stirling, or Otto cycles. Given additional irreversible processes this evolutionary scheme learns a hitherto unknown thermodynamic cycle. Our results show how the reinforcement learning strategies developed for game playing can be applied to solve physical problems conditioned upon path-extensive order parameters.