Weakly-supervised multi-class object localization using only object counts as labels

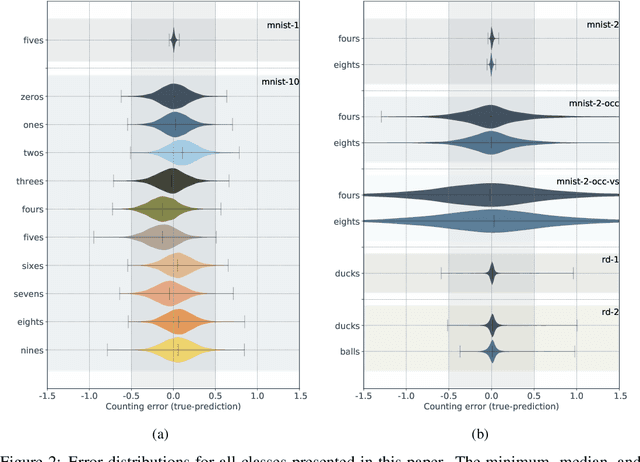
We demonstrate the use of an extensive deep neural network to localize instances of objects in images. The EDNN is naturally able to accurately perform multi-class counting using only ground truth count values as labels. Without providing any conceptual information, object annotations, or pixel segmentation information, the neural network is able to formulate its own conceptual representation of the items in the image. Using images labelled with only the counts of the objects present,the structure of the extensive deep neural network can be exploited to perform localization of the objects within the visual field. We demonstrate that a trained EDNN can be used to count objects in images much larger than those on which it was trained. In order to demonstrate our technique, we introduce seven new data sets: five progressively harder MNIST digit-counting data sets, and two datasets of 3d-rendered rubber ducks in various situations. On most of these datasets, the EDNN achieves greater than 99% test set accuracy in counting objects.

Optimizing thermodynamic trajectories using evolutionary reinforcement learning

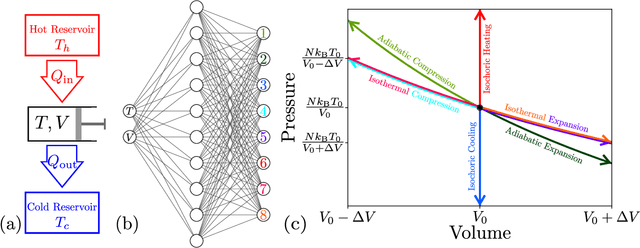
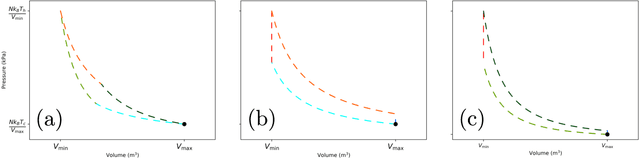
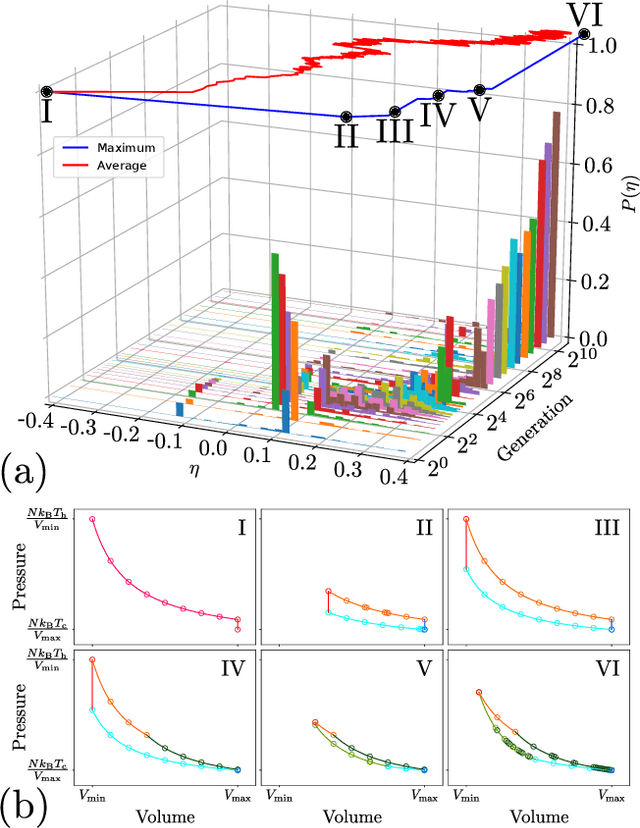
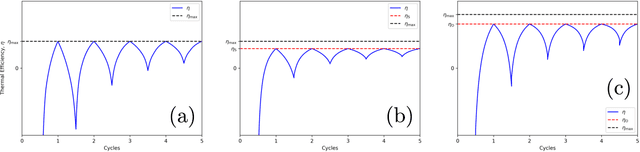
Using a model heat engine we show that neural network-based reinforcement learning can identify thermodynamic trajectories of maximal efficiency. We use an evolutionary learning algorithm to evolve a population of neural networks, subject to a directive to maximize the efficiency of a trajectory composed of a set of elementary thermodynamic processes; the resulting networks learn to carry out the maximally-efficient Carnot, Stirling, or Otto cycles. Given additional irreversible processes this evolutionary scheme learns a hitherto unknown thermodynamic cycle. Our results show how the reinforcement learning strategies developed for game playing can be applied to solve physical problems conditioned upon path-extensive order parameters.

Deep learning and the Schrödinger equation

We have trained a deep (convolutional) neural network to predict the ground-state energy of an electron in four classes of confining two-dimensional electrostatic potentials. On randomly generated potentials, for which there is no analytic form for either the potential or the ground-state energy, the neural network model was able to predict the ground-state energy to within chemical accuracy, with a median absolute error of 1.49 mHa. We also investigate the performance of the model in predicting other quantities such as the kinetic energy and the first excited-state energy of random potentials.