Optimizing thermodynamic trajectories using evolutionary reinforcement learning

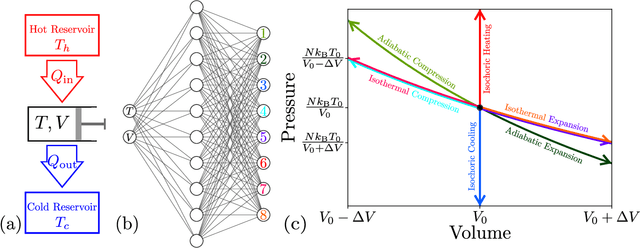
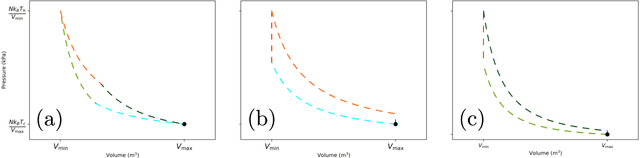
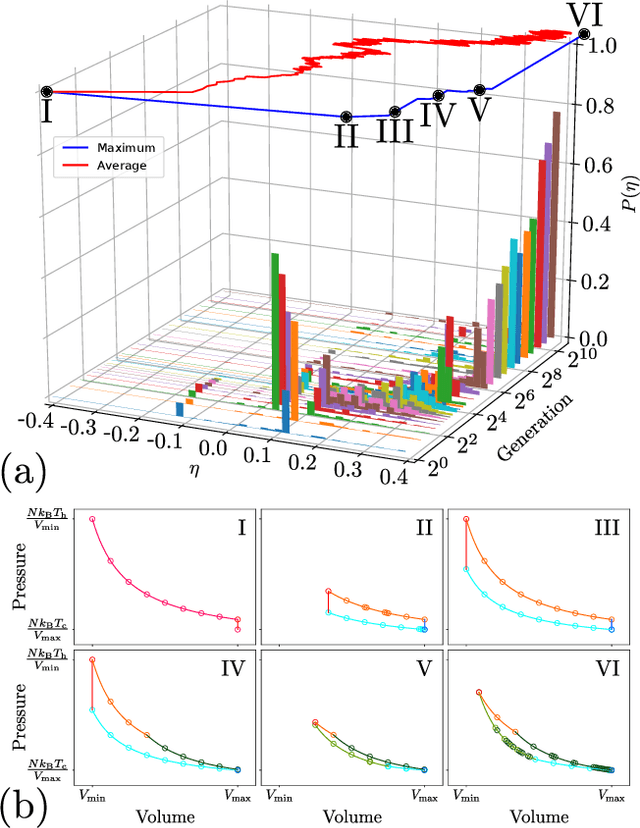
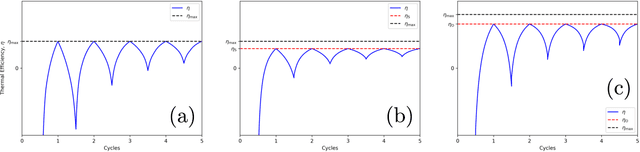
Using a model heat engine we show that neural network-based reinforcement learning can identify thermodynamic trajectories of maximal efficiency. We use an evolutionary learning algorithm to evolve a population of neural networks, subject to a directive to maximize the efficiency of a trajectory composed of a set of elementary thermodynamic processes; the resulting networks learn to carry out the maximally-efficient Carnot, Stirling, or Otto cycles. Given additional irreversible processes this evolutionary scheme learns a hitherto unknown thermodynamic cycle. Our results show how the reinforcement learning strategies developed for game playing can be applied to solve physical problems conditioned upon path-extensive order parameters.