A Game-Theoretic Analysis of the Empirical Revenue Maximization Algorithm with Endogenous Sampling

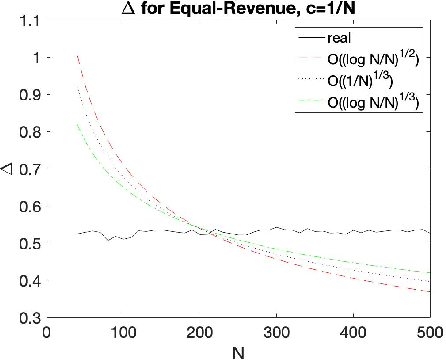
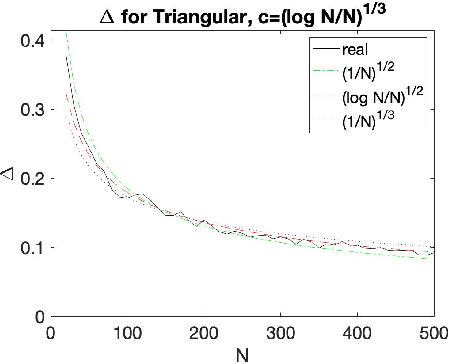
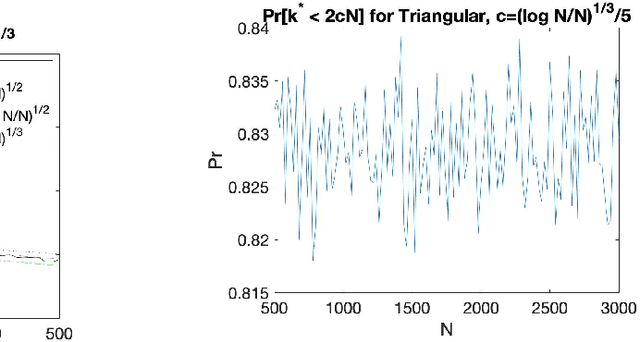
The Empirical Revenue Maximization (ERM) is one of the most important price learning algorithms in auction design: as the literature shows it can learn approximately optimal reserve prices for revenue-maximizing auctioneers in both repeated auctions and uniform-price auctions. However, in these applications the agents who provide inputs to ERM have incentives to manipulate the inputs to lower the outputted price. We generalize the definition of an incentive-awareness measure proposed by Lavi et al (2019), to quantify the reduction of ERM's outputted price due to a change of $m\ge 1$ out of $N$ input samples, and provide specific convergence rates of this measure to zero as $N$ goes to infinity for different types of input distributions. By adopting this measure, we construct an efficient, approximately incentive-compatible, and revenue-optimal learning algorithm using ERM in repeated auctions against non-myopic bidders, and show approximate group incentive-compatibility in uniform-price auctions.

Deterministic Leader Election in Programmable Matter

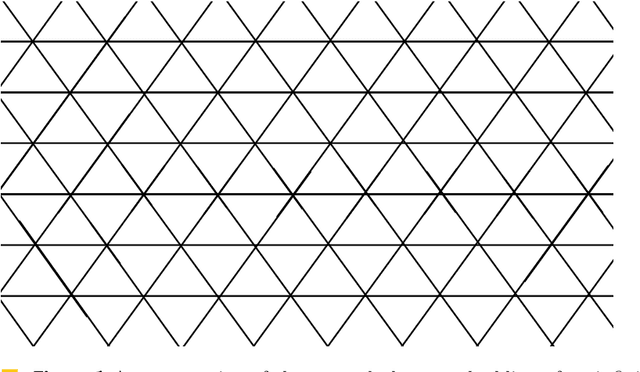
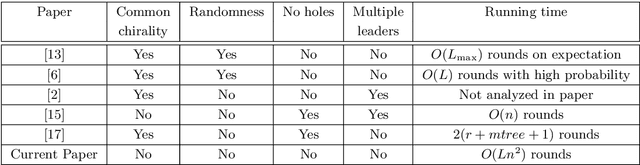
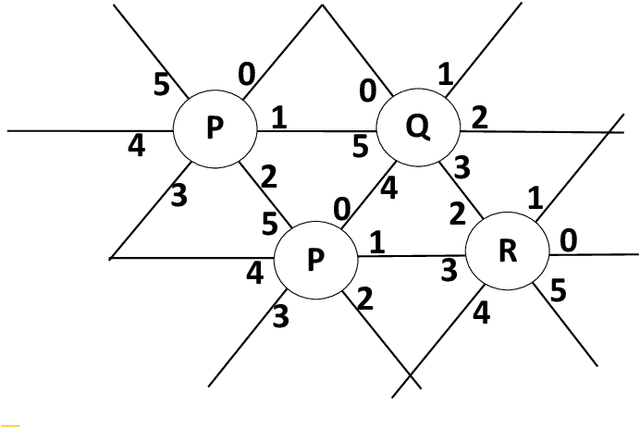
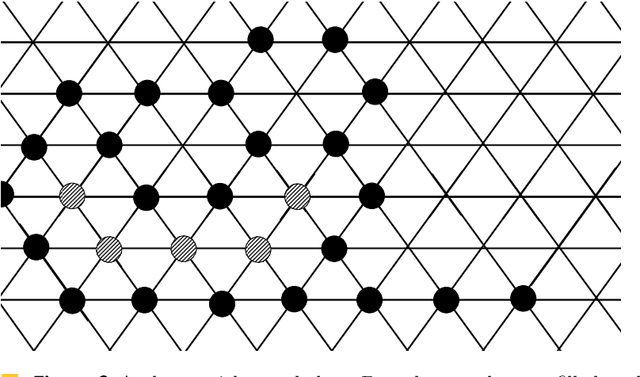
Addressing a fundamental problem in programmable matter, we present the first deterministic algorithm to elect a unique leader in a system of connected amoebots assuming only that amoebots are initially contracted. Previous algorithms either used randomization, made various assumptions (shapes with no holes, or known shared chirality), or elected several co-leaders in some cases. Some of the building blocks we introduce in constructing the algorithm are of interest by themselves, especially the procedure we present for reaching common chirality among the amoebots. Given the leader election and the chirality agreement building block, it is known that various tasks in programmable matter can be performed or improved. The main idea of the new algorithm is the usage of the ability of the amoebots to move, which previous leader election algorithms have not used.