Shay Kutten
Online Paging with a Vanishing Regret
Nov 19, 2020Abstract:This paper considers a variant of the online paging problem, where the online algorithm has access to multiple predictors, each producing a sequence of predictions for the page arrival times. The predictors may have occasional prediction errors and it is assumed that at least one of them makes a sublinear number of prediction errors in total. Our main result states that this assumption suffices for the design of a randomized online algorithm whose time-average regret with respect to the optimal offline algorithm tends to zero as the time tends to infinity. This holds (with different regret bounds) for both the full information access model, where in each round, the online algorithm gets the predictions of all predictors, and the bandit access model, where in each round, the online algorithm queries a single predictor. While online algorithms that exploit inaccurate predictions have been a topic of growing interest in the last few years, to the best of our knowledge, this is the first paper that studies this topic in the context of multiple predictors for an online problem with unbounded request sequences. Moreover, to the best of our knowledge, this is also the first paper that aims for (and achieves) online algorithms with a vanishing regret for a classic online problem under reasonable assumptions.
Deterministic Leader Election in Programmable Matter
May 02, 2019
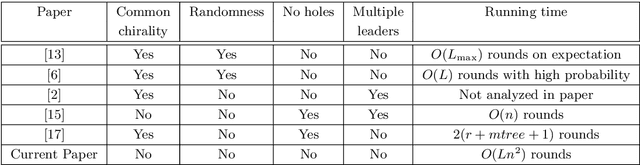
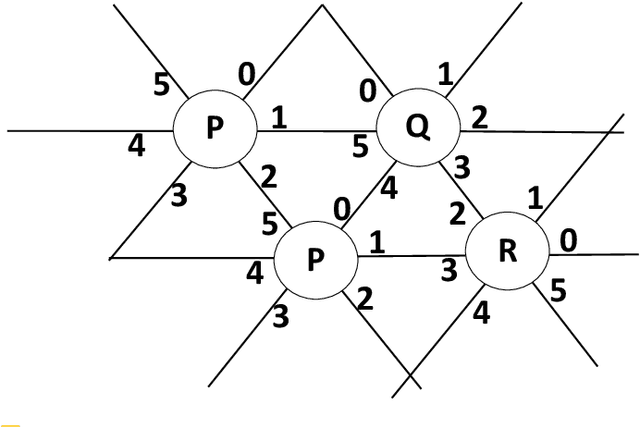
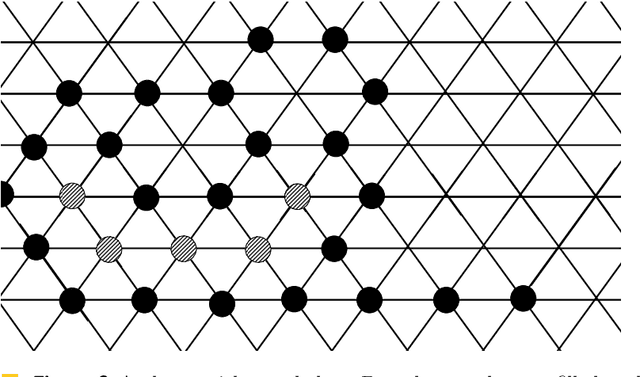
Abstract:Addressing a fundamental problem in programmable matter, we present the first deterministic algorithm to elect a unique leader in a system of connected amoebots assuming only that amoebots are initially contracted. Previous algorithms either used randomization, made various assumptions (shapes with no holes, or known shared chirality), or elected several co-leaders in some cases. Some of the building blocks we introduce in constructing the algorithm are of interest by themselves, especially the procedure we present for reaching common chirality among the amoebots. Given the leader election and the chirality agreement building block, it is known that various tasks in programmable matter can be performed or improved. The main idea of the new algorithm is the usage of the ability of the amoebots to move, which previous leader election algorithms have not used.
Fast Rendezvous on a Cycle by Agents with Different Speeds
Sep 13, 2015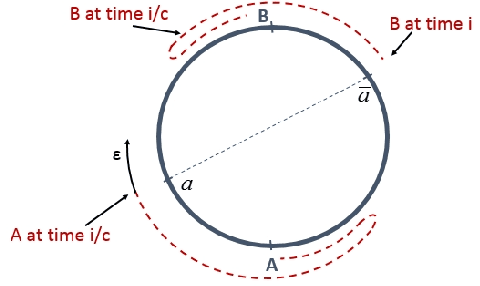
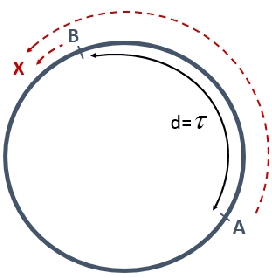
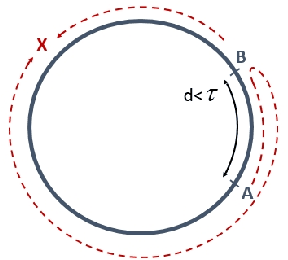
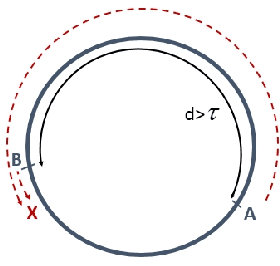
Abstract:The difference between the speed of the actions of different processes is typically considered as an obstacle that makes the achievement of cooperative goals more difficult. In this work, we aim to highlight potential benefits of such asynchrony phenomena to tasks involving symmetry breaking. Specifically, in this paper, identical (except for their speeds) mobile agents are placed at arbitrary locations on a cycle of length $n$ and use their speed difference in order to rendezvous fast. We normalize the speed of the slower agent to be 1, and fix the speed of the faster agent to be some $c>1$. (An agent does not know whether it is the slower agent or the faster one.) The straightforward distributed-race DR algorithm is the one in which both agents simply start walking until rendezvous is achieved. It is easy to show that, in the worst case, the rendezvous time of DR is $n/(c-1)$. Note that in the interesting case, where $c$ is very close to 1 this bound becomes huge. Our first result is a lower bound showing that, up to a multiplicative factor of 2, this bound is unavoidable, even in a model that allows agents to leave arbitrary marks, even assuming sense of direction, and even assuming $n$ and $c$ are known to agents. That is, we show that under such assumptions, the rendezvous time of any algorithm is at least $\frac{n}{2(c-1)}$ if $c\leq 3$ and slightly larger if $c>3$. We then construct an algorithm that precisely matches the lower bound for the case $c\leq 2$, and almost matches it when $c>2$. Moreover, our algorithm performs under weaker assumptions than those stated above, as it does not assume sense of direction, and it allows agents to leave only a single mark (a pebble) and only at the place where they start the execution. Finally, we investigate the setting in which no marks can be used at all, and show tight bounds for $c\leq 2$, and almost tight bounds for $c>2$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge