The Dependent Doors Problem: An Investigation into Sequential Decisions without Feedback

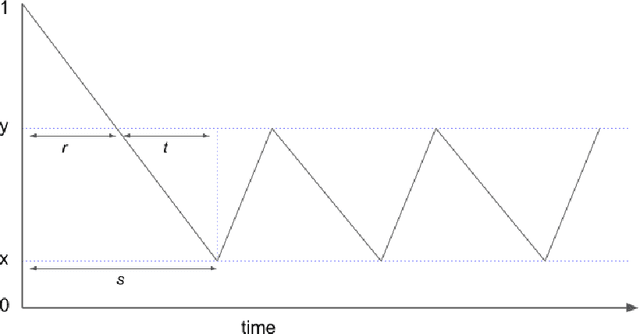
We introduce the dependent doors problem as an abstraction for situations in which one must perform a sequence of possibly dependent decisions, without receiving feedback information on the effectiveness of previously made actions. Informally, the problem considers a set of $d$ doors that are initially closed, and the aim is to open all of them as fast as possible. To open a door, the algorithm knocks on it and it might open or not according to some probability distribution. This distribution may depend on which other doors are currently open, as well as on which other doors were open during each of the previous knocks on that door. The algorithm aims to minimize the expected time until all doors open. Crucially, it must act at any time without knowing whether or which other doors have already opened. In this work, we focus on scenarios where dependencies between doors are both positively correlated and acyclic.The fundamental distribution of a door describes the probability it opens in the best of conditions (with respect to other doors being open or closed). We show that if in two configurations of $d$ doors corresponding doors share the same fundamental distribution, then these configurations have the same optimal running time up to a universal constant, no matter what are the dependencies between doors and what are the distributions. We also identify algorithms that are optimal up to a universal constant factor. For the case in which all doors share the same fundamental distribution we additionally provide a simpler algorithm, and a formula to calculate its running time. We furthermore analyse the price of lacking feedback for several configurations governed by standard fundamental distributions. In particular, we show that the price is logarithmic in $d$ for memoryless doors, but can potentially grow to be linear in $d$ for other distributions.We then turn our attention to investigate precise bounds. Even for the case of two doors, identifying the optimal sequence is an intriguing combinatorial question. Here, we study the case of two cascading memoryless doors. That is, the first door opens on each knock independently with probability $p\_1$. The second door can only open if the first door is open, in which case it will open on each knock independently with probability $p\_2$. We solve this problem almost completely by identifying algorithms that are optimal up to an additive term of 1.

Fast Rendezvous on a Cycle by Agents with Different Speeds

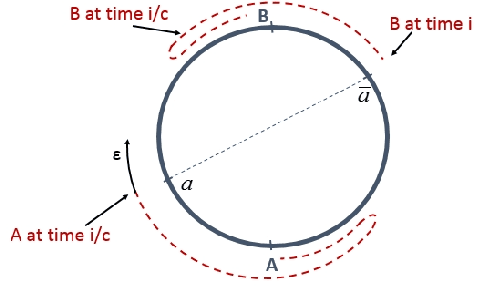
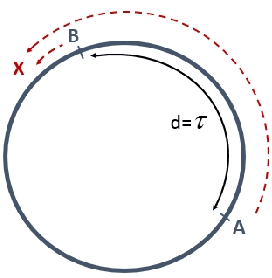
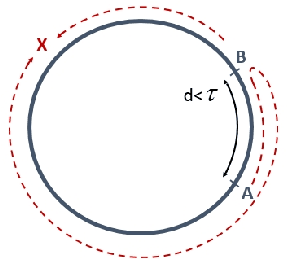
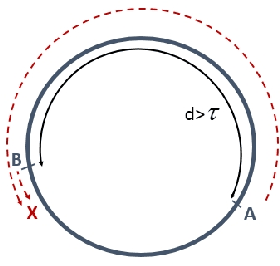
The difference between the speed of the actions of different processes is typically considered as an obstacle that makes the achievement of cooperative goals more difficult. In this work, we aim to highlight potential benefits of such asynchrony phenomena to tasks involving symmetry breaking. Specifically, in this paper, identical (except for their speeds) mobile agents are placed at arbitrary locations on a cycle of length $n$ and use their speed difference in order to rendezvous fast. We normalize the speed of the slower agent to be 1, and fix the speed of the faster agent to be some $c>1$. (An agent does not know whether it is the slower agent or the faster one.) The straightforward distributed-race DR algorithm is the one in which both agents simply start walking until rendezvous is achieved. It is easy to show that, in the worst case, the rendezvous time of DR is $n/(c-1)$. Note that in the interesting case, where $c$ is very close to 1 this bound becomes huge. Our first result is a lower bound showing that, up to a multiplicative factor of 2, this bound is unavoidable, even in a model that allows agents to leave arbitrary marks, even assuming sense of direction, and even assuming $n$ and $c$ are known to agents. That is, we show that under such assumptions, the rendezvous time of any algorithm is at least $\frac{n}{2(c-1)}$ if $c\leq 3$ and slightly larger if $c>3$. We then construct an algorithm that precisely matches the lower bound for the case $c\leq 2$, and almost matches it when $c>2$. Moreover, our algorithm performs under weaker assumptions than those stated above, as it does not assume sense of direction, and it allows agents to leave only a single mark (a pebble) and only at the place where they start the execution. Finally, we investigate the setting in which no marks can be used at all, and show tight bounds for $c\leq 2$, and almost tight bounds for $c>2$.