Fast Rendezvous on a Cycle by Agents with Different Speeds
Paper and Code
Sep 13, 2015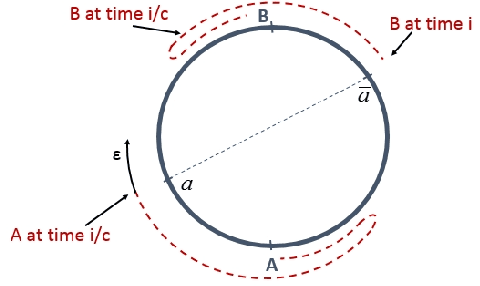
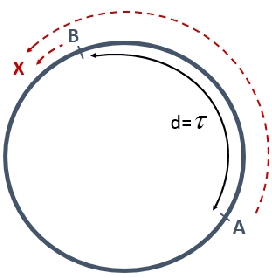
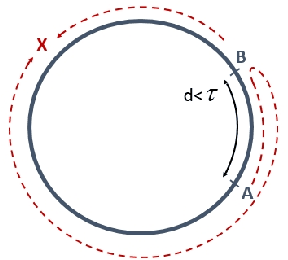
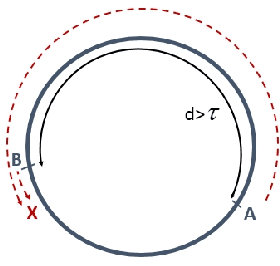
The difference between the speed of the actions of different processes is typically considered as an obstacle that makes the achievement of cooperative goals more difficult. In this work, we aim to highlight potential benefits of such asynchrony phenomena to tasks involving symmetry breaking. Specifically, in this paper, identical (except for their speeds) mobile agents are placed at arbitrary locations on a cycle of length $n$ and use their speed difference in order to rendezvous fast. We normalize the speed of the slower agent to be 1, and fix the speed of the faster agent to be some $c>1$. (An agent does not know whether it is the slower agent or the faster one.) The straightforward distributed-race DR algorithm is the one in which both agents simply start walking until rendezvous is achieved. It is easy to show that, in the worst case, the rendezvous time of DR is $n/(c-1)$. Note that in the interesting case, where $c$ is very close to 1 this bound becomes huge. Our first result is a lower bound showing that, up to a multiplicative factor of 2, this bound is unavoidable, even in a model that allows agents to leave arbitrary marks, even assuming sense of direction, and even assuming $n$ and $c$ are known to agents. That is, we show that under such assumptions, the rendezvous time of any algorithm is at least $\frac{n}{2(c-1)}$ if $c\leq 3$ and slightly larger if $c>3$. We then construct an algorithm that precisely matches the lower bound for the case $c\leq 2$, and almost matches it when $c>2$. Moreover, our algorithm performs under weaker assumptions than those stated above, as it does not assume sense of direction, and it allows agents to leave only a single mark (a pebble) and only at the place where they start the execution. Finally, we investigate the setting in which no marks can be used at all, and show tight bounds for $c\leq 2$, and almost tight bounds for $c>2$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge