A Game-Theoretic Analysis of the Empirical Revenue Maximization Algorithm with Endogenous Sampling
Paper and Code
Oct 12, 2020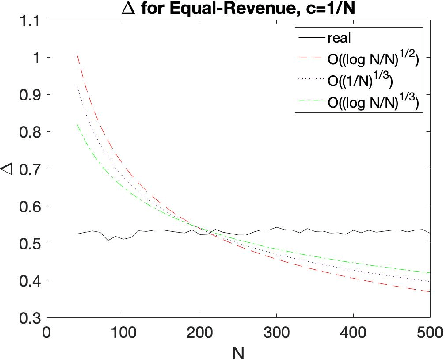

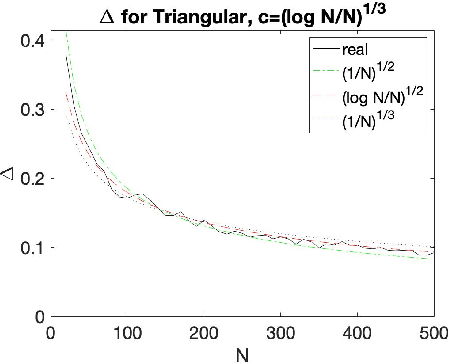
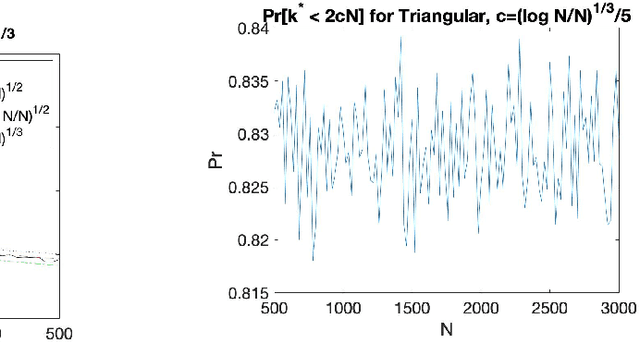
The Empirical Revenue Maximization (ERM) is one of the most important price learning algorithms in auction design: as the literature shows it can learn approximately optimal reserve prices for revenue-maximizing auctioneers in both repeated auctions and uniform-price auctions. However, in these applications the agents who provide inputs to ERM have incentives to manipulate the inputs to lower the outputted price. We generalize the definition of an incentive-awareness measure proposed by Lavi et al (2019), to quantify the reduction of ERM's outputted price due to a change of $m\ge 1$ out of $N$ input samples, and provide specific convergence rates of this measure to zero as $N$ goes to infinity for different types of input distributions. By adopting this measure, we construct an efficient, approximately incentive-compatible, and revenue-optimal learning algorithm using ERM in repeated auctions against non-myopic bidders, and show approximate group incentive-compatibility in uniform-price auctions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge