Obtaining Example-Based Explanations from Deep Neural Networks

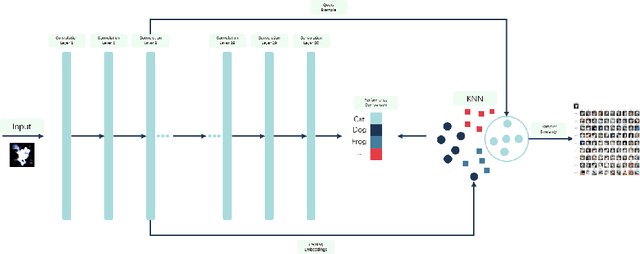
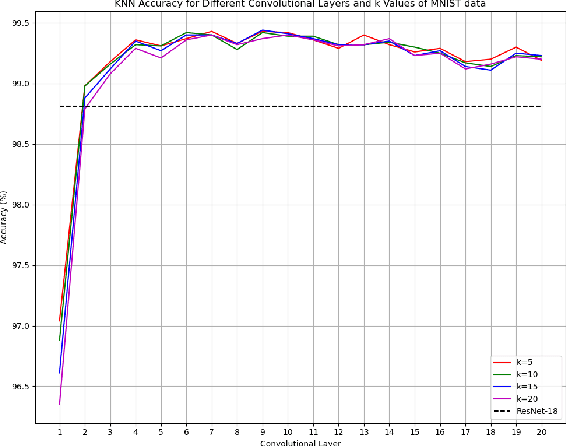
Most techniques for explainable machine learning focus on feature attribution, i.e., values are assigned to the features such that their sum equals the prediction. Example attribution is another form of explanation that assigns weights to the training examples, such that their scalar product with the labels equals the prediction. The latter may provide valuable complementary information to feature attribution, in particular in cases where the features are not easily interpretable. Current example-based explanation techniques have targeted a few model types only, such as k-nearest neighbors and random forests. In this work, a technique for obtaining example-based explanations from deep neural networks (EBE-DNN) is proposed. The basic idea is to use the deep neural network to obtain an embedding, which is employed by a k-nearest neighbor classifier to form a prediction; the example attribution can hence straightforwardly be derived from the latter. Results from an empirical investigation show that EBE-DNN can provide highly concentrated example attributions, i.e., the predictions can be explained with few training examples, without reducing accuracy compared to the original deep neural network. Another important finding from the empirical investigation is that the choice of layer to use for the embeddings may have a large impact on the resulting accuracy.

KAGNNs: Kolmogorov-Arnold Networks meet Graph Learning

In recent years, Graph Neural Networks (GNNs) have become the de facto tool for learning node and graph representations. Most GNNs typically consist of a sequence of neighborhood aggregation (a.k.a., message passing) layers. Within each of these layers, the representation of each node is updated from an aggregation and transformation of its neighbours representations at the previous layer. The upper bound for the expressive power of message passing GNNs was reached through the use of MLPs as a transformation, due to their universal approximation capabilities. However, MLPs suffer from well-known limitations, which recently motivated the introduction of Kolmogorov-Arnold Networks (KANs). KANs rely on the Kolmogorov-Arnold representation theorem, rendering them a promising alternative to MLPs. In this work, we compare the performance of KANs against that of MLPs in graph learning tasks. We perform extensive experiments on node classification, graph classification and graph regression datasets. Our preliminary results indicate that while KANs are on-par with MLPs in classification tasks, they seem to have a clear advantage in the graph regression tasks.