Towards a Decentralized, Autonomous Multiagent Framework for Mitigating Crop Loss

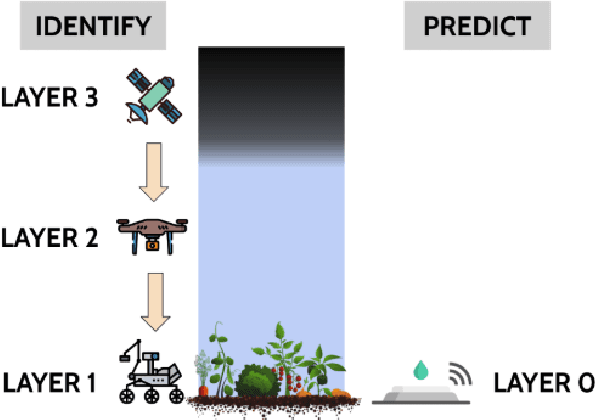
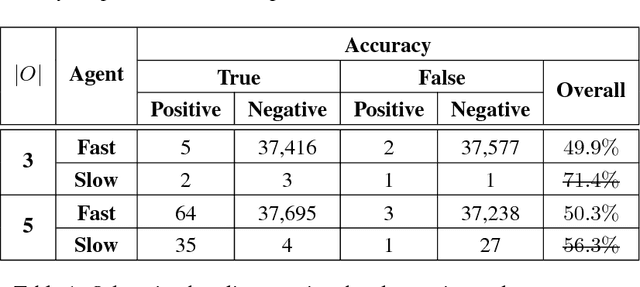
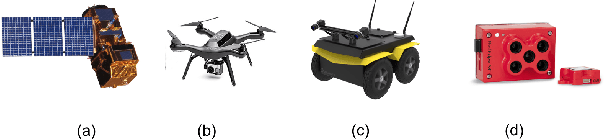
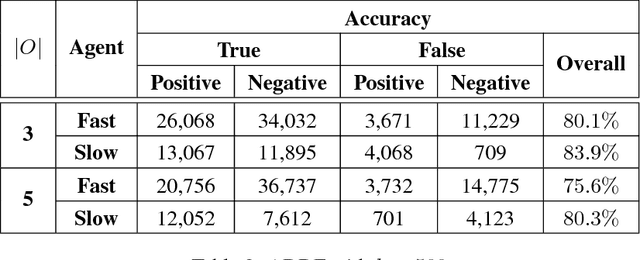
We propose a generalized decision-theoretic system for a heterogeneous team of autonomous agents who are tasked with online identification of phenotypically expressed stress in crop fields.. This system employs four distinct types of agents, specific to four available sensor modalities: satellites (Layer 3), uninhabited aerial vehicles (L2), uninhabited ground vehicles (L1), and static ground-level sensors (L0). Layers 3, 2, and 1 are tasked with performing image processing at the available resolution of the sensor modality and, along with data generated by layer 0 sensors, identify erroneous differences that arise over time. Our goal is to limit the use of the more computationally and temporally expensive subsequent layers. Therefore, from layer 3 to 1, each layer only investigates areas that previous layers have identified as potentially afflicted by stress. We introduce a reinforcement learning technique based on Perkins' Monte Carlo Exploring Starts for a generalized Markovian model for each layer's decision problem, and label the system the Agricultural Distributed Decision Framework (ADDF). As our domain is real-world and online, we illustrate implementations of the two major components of our system: a clustering-based image processing methodology and a two-layer POMDP implementation.

Optimal Decision-Making in Mixed-Agent Partially Observable Stochastic Environments via Reinforcement Learning

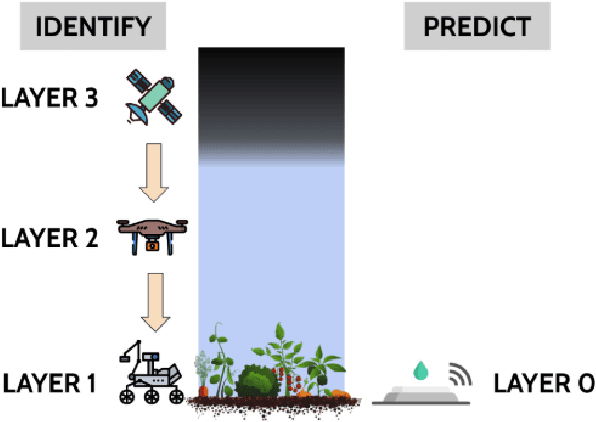
Optimal decision making with limited or no information in stochastic environments where multiple agents interact is a challenging topic in the realm of artificial intelligence. Reinforcement learning (RL) is a popular approach for arriving at optimal strategies by predicating stimuli, such as the reward for following a strategy, on experience. RL is heavily explored in the single-agent context, but is a nascent concept in multiagent problems. To this end, I propose several principled model-free and partially model-based reinforcement learning approaches for several multiagent settings. In the realm of normative reinforcement learning, I introduce scalable extensions to Monte Carlo exploring starts for partially observable Markov Decision Processes (POMDP), dubbed MCES-P, where I expand the theory and algorithm to the multiagent setting. I first examine MCES-P with probably approximately correct (PAC) bounds in the context of multiagent setting, showing MCESP+PAC holds in the presence of other agents. I then propose a more sample-efficient methodology for antagonistic settings, MCESIP+PAC. For cooperative settings, I extend MCES-P to the Multiagent POMDP, dubbed MCESMP+PAC. I then explore the use of reinforcement learning as a methodology in searching for optima in realistic and latent model environments. First, I explore a parameterized Q-learning approach in modeling humans learning to reason in an uncertain, multiagent environment. Next, I propose an implementation of MCES-P, along with image segmentation, to create an adaptive team-based reinforcement learning technique to positively identify the presence of phenotypically-expressed water and pathogen stress in crop fields.

Reinforcement Learning for Heterogeneous Teams with PALO Bounds

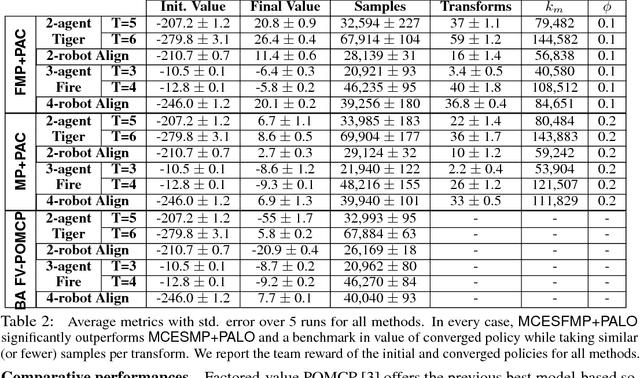
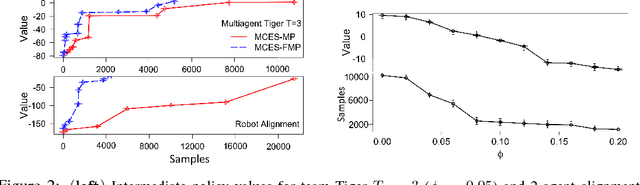
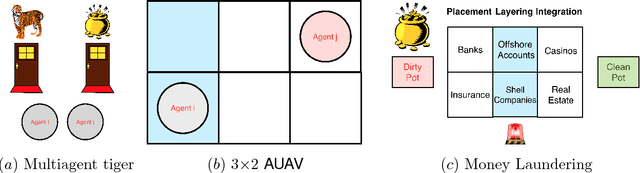
We introduce reinforcement learning for heterogeneous teams in which rewards for an agent are additively factored into local costs, stimuli unique to each agent, and global rewards, those shared by all agents in the domain. Motivating domains include coordination of varied robotic platforms, which incur different costs for the same action, but share an overall goal. We present two templates for learning in this setting with factored rewards: a generalization of Perkins' Monte Carlo exploring starts for POMDPs to canonical MPOMDPs, with a single policy mapping joint observations of all agents to joint actions (MCES-MP); and another with each agent individually mapping joint observations to their own action (MCES-FMP). We use probably approximately local optimal (PALO) bounds to analyze sample complexity, instantiating these templates to PALO learning. We promote sample efficiency by including a policy space pruning technique, and evaluate the approaches on three domains of heterogeneous agents demonstrating that MCES-FMP yields improved policies in less samples compared to MCES-MP and a previous benchmark.