Reinforcement Learning for Heterogeneous Teams with PALO Bounds
Paper and Code
May 23, 2018
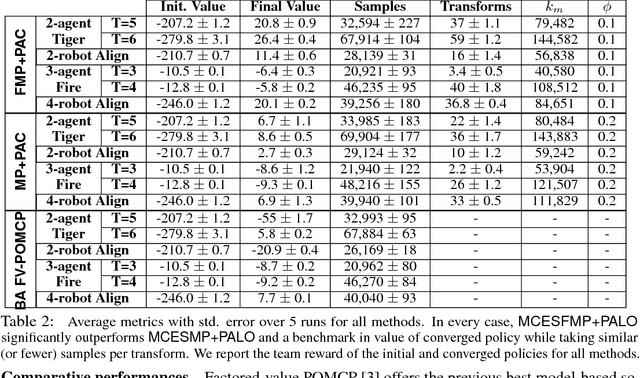
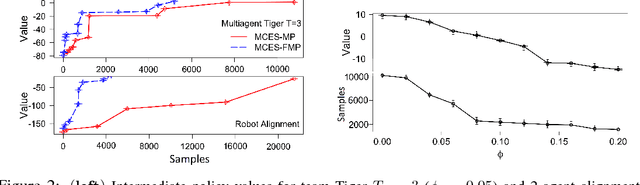
We introduce reinforcement learning for heterogeneous teams in which rewards for an agent are additively factored into local costs, stimuli unique to each agent, and global rewards, those shared by all agents in the domain. Motivating domains include coordination of varied robotic platforms, which incur different costs for the same action, but share an overall goal. We present two templates for learning in this setting with factored rewards: a generalization of Perkins' Monte Carlo exploring starts for POMDPs to canonical MPOMDPs, with a single policy mapping joint observations of all agents to joint actions (MCES-MP); and another with each agent individually mapping joint observations to their own action (MCES-FMP). We use probably approximately local optimal (PALO) bounds to analyze sample complexity, instantiating these templates to PALO learning. We promote sample efficiency by including a policy space pruning technique, and evaluate the approaches on three domains of heterogeneous agents demonstrating that MCES-FMP yields improved policies in less samples compared to MCES-MP and a previous benchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge