SIMAP: A simplicial-map layer for neural networks

In this paper, we present SIMAP, a novel layer integrated into deep learning models, aimed at enhancing the interpretability of the output. The SIMAP layer is an enhanced version of Simplicial-Map Neural Networks (SMNNs), an explainable neural network based on support sets and simplicial maps (functions used in topology to transform shapes while preserving their structural connectivity). The novelty of the methodology proposed in this paper is two-fold: Firstly, SIMAP layers work in combination with other deep learning architectures as an interpretable layer substituting classic dense final layers. Secondly, unlike SMNNs, the support set is based on a fixed maximal simplex, the barycentric subdivision being efficiently computed with a matrix-based multiplication algorithm.

A Topological Approach to Measuring Training Data Quality

Data quality is crucial for the successful training, generalization and performance of artificial intelligence models. Furthermore, it is known that the leading approaches in artificial intelligence are notoriously data-hungry. In this paper, we propose the use of small training datasets towards faster training. Specifically, we provide a novel topological method based on morphisms between persistence modules to measure the training data quality with respect to the complete dataset. This way, we can provide an explanation of why the chosen training dataset will lead to poor performance.

Explainability in Simplicial Map Neural Networks

Simplicial map neural networks (SMNNs) are topology-based neural networks with interesting properties such as universal approximation capability and robustness to adversarial examples under appropriate conditions. However, SMNNs present some bottlenecks for their possible application in high dimensions. First, no SMNN training process has been defined so far. Second, SMNNs require the construction of a convex polytope surrounding the input dataset. In this paper, we propose a SMNN training procedure based on a support subset of the given dataset and a method based on projection to a hypersphere as a replacement for the convex polytope construction. In addition, the explainability capacity of SMNNs is also introduced for the first time in this paper.

Emotion recognition in talking-face videos using persistent entropy and neural networks

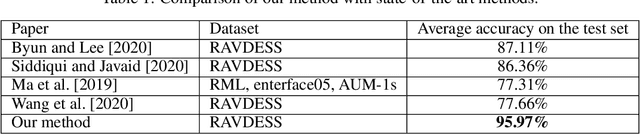
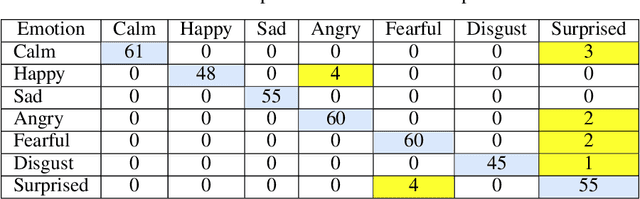
The automatic recognition of a person's emotional state has become a very active research field that involves scientists specialized in different areas such as artificial intelligence, computer vision or psychology, among others. Our main objective in this work is to develop a novel approach, using persistent entropy and neural networks as main tools, to recognise and classify emotions from talking-face videos. Specifically, we combine audio-signal and image-sequence information to compute a topology signature(a 9-dimensional vector) for each video. We prove that small changes in the video produce small changes in the signature. These topological signatures are used to feed a neural network to distinguish between the following emotions: neutral, calm, happy, sad, angry, fearful, disgust, and surprised. The results reached are promising and competitive, beating the performance reached in other state-of-the-art works found in the literature.

Towards a Philological Metric through a Topological Data Analysis Approach

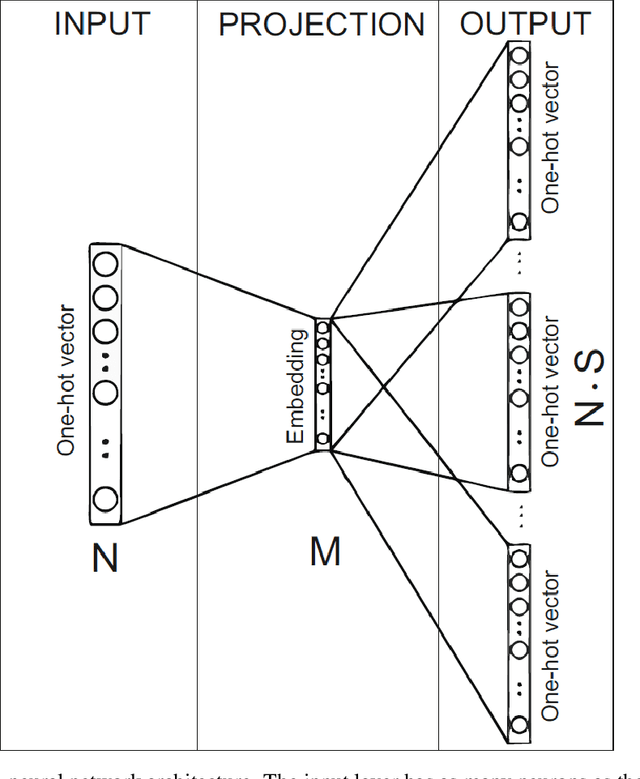
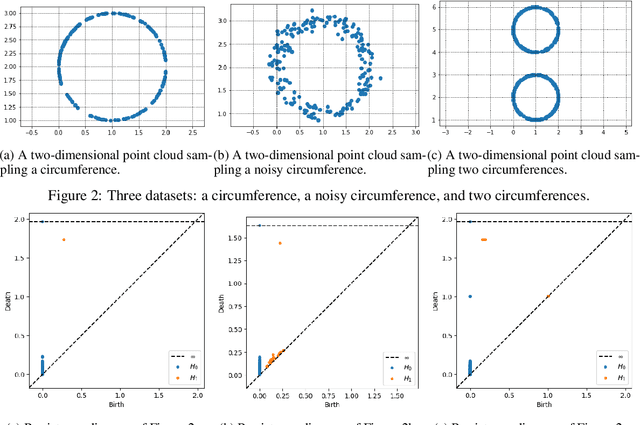
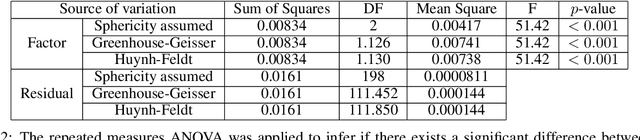
The canon of the baroque Spanish literature has been thoroughly studied with philological techniques. The major representatives of the poetry of this epoch are Francisco de Quevedo and Luis de G\'ongora y Argote. They are commonly classified by the literary experts in two different streams: Quevedo belongs to the Conceptismo and G\'ongora to the Culteranismo. Besides, traditionally, even if Quevedo is considered the most representative of the Conceptismo, Lope de Vega is also considered to be, at least, closely related to this literary trend. In this paper, we use Topological Data Analysis techniques to provide a first approach to a metric distance between the literary style of these poets. As a consequence, we reach results that are under the literary experts' criteria, locating the literary style of Lope de Vega, closer to the one of Quevedo than to the one of G\'ongora.

Two-hidden-layer Feedforward Neural Networks are Universal Approximators: A Constructive Approach

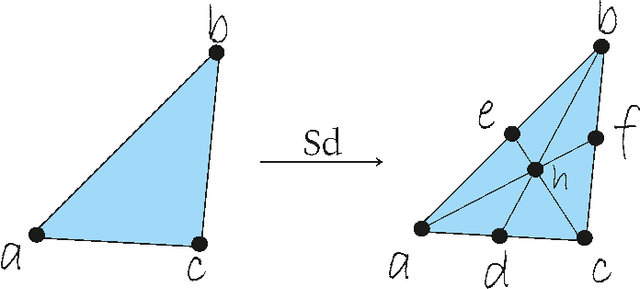
It is well known that Artificial Neural Networks are universal approximators. The classical result proves that, given a continuous function on a compact set on an n-dimensional space, then there exists a one-hidden-layer feedforward network which approximates the function. Such result proves the existence, but it does not provide a method for finding it. In this paper, a constructive approach to the proof of this property is given for the case of two-hidden-layer feedforward networks. This approach is based on an approximation of continuous functions by simplicial maps. Once a triangulation of the space is given, a concrete architecture and set of weights can be obtained. The quality of the approximation depends on the refinement of the covering of the space by simplicial complexes.

Topological signature for periodic motion recognition

In this paper, we present an algorithm that computes the topological signature for a given periodic motion sequence. Such signature consists of a vector obtained by persistent homology which captures the topological and geometric changes of the object that models the motion. Two topological signatures are compared simply by the angle between the corresponding vectors. With respect to gait recognition, we have tested our method using only the lowest fourth part of the body's silhouette. In this way, the impact of variations in the upper part of the body, which are very frequent in real scenarios, decreases considerably. We have also tested our method using other periodic motions such as running or jumping. Finally, we formally prove that our method is robust to small perturbations in the input data and does not depend on the number of periods contained in the periodic motion sequence.

Representative Datasets: The Perceptron Case

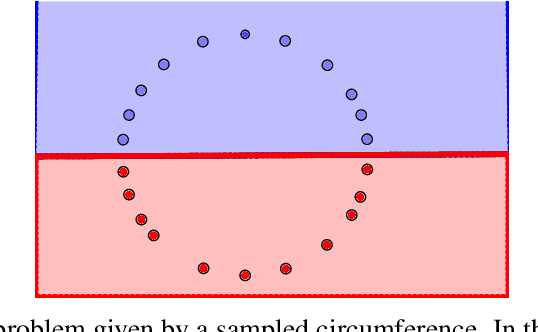
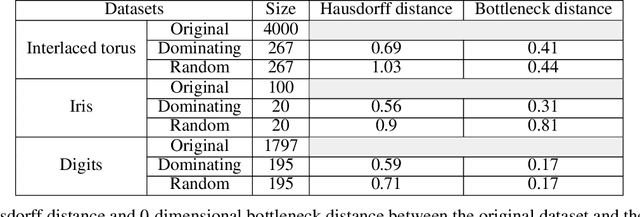
One of the main drawbacks of the practical use of neural networks is the long time needed in the training process. Such training process consists in an iterative change of parameters trying to minimize a loss function. These changes are driven by a dataset, which can be seen as a set of labeled points in an n-dimensional space. In this paper, we explore the concept of it representative dataset which is smaller than the original dataset and satisfies a nearness condition independent of isometric transformations. The representativeness is measured using persistence diagrams due to its computational efficiency. We also prove that the accuracy of the learning process of a neural network on a representative dataset is comparable with the accuracy on the original dataset when the neural network architecture is a perceptron and the loss function is the mean squared error. These theoretical results accompanied with experimentation open a door to the size reduction of the dataset in order to gain time in the training process of any neural network.

Topological Tracking of Connected Components in Image Sequences

Persistent homology provides information about the lifetime of homology classes along a filtration of cell complexes. Persistence barcode is a graphical representation of such information. A filtration might be determined by time in a set of spatiotemporal data, but classical methods for computing persistent homology do not respect the fact that we can not move backwards in time. In this paper, taking as input a time-varying sequence of two-dimensional (2D) binary digital images, we develop an algorithm for encoding, in the so-called {\it spatiotemporal barcode}, lifetime of connected components (of either the foreground or background) that are moving in the image sequence over time (this information may not coincide with the one provided by the persistence barcode). This way, given a connected component at a specific time in the sequence, we can track the component backwards in time until the moment it was born, by what we call a {\it spatiotemporal path}. The main contribution of this paper with respect to our previous works lies in a new algorithm that computes spatiotemporal paths directly, valid for both foreground and background and developed in a general context, setting the ground for a future extension for tracking higher dimensional topological features in $nD$ binary digital image sequences.

Removal and Contraction Operations in $n$D Generalized Maps for Efficient Homology Computation

In this paper, we show that contraction operations preserve the homology of $n$D generalized maps, under some conditions. Removal and contraction operations are used to propose an efficient algorithm that compute homology generators of $n$D generalized maps. Its principle consists in simplifying a generalized map as much as possible by using removal and contraction operations. We obtain a generalized map having the same homology than the initial one, while the number of cells decreased significantly. Keywords: $n$D Generalized Maps; Cellular Homology; Homology Generators; Contraction and Removal Operations.