Representative Datasets: The Perceptron Case

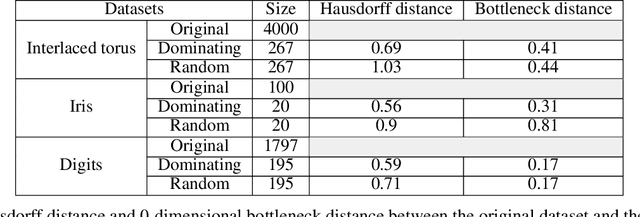
One of the main drawbacks of the practical use of neural networks is the long time needed in the training process. Such training process consists in an iterative change of parameters trying to minimize a loss function. These changes are driven by a dataset, which can be seen as a set of labeled points in an n-dimensional space. In this paper, we explore the concept of it representative dataset which is smaller than the original dataset and satisfies a nearness condition independent of isometric transformations. The representativeness is measured using persistence diagrams due to its computational efficiency. We also prove that the accuracy of the learning process of a neural network on a representative dataset is comparable with the accuracy on the original dataset when the neural network architecture is a perceptron and the loss function is the mean squared error. These theoretical results accompanied with experimentation open a door to the size reduction of the dataset in order to gain time in the training process of any neural network.