Application of the representative measure approach to assess the reliability of decision trees in dealing with unseen vehicle collision data

Machine learning algorithms are fundamental components of novel data-informed Artificial Intelligence architecture. In this domain, the imperative role of representative datasets is a cornerstone in shaping the trajectory of artificial intelligence (AI) development. Representative datasets are needed to train machine learning components properly. Proper training has multiple impacts: it reduces the final model's complexity, power, and uncertainties. In this paper, we investigate the reliability of the $\varepsilon$-representativeness method to assess the dataset similarity from a theoretical perspective for decision trees. We decided to focus on the family of decision trees because it includes a wide variety of models known to be explainable. Thus, in this paper, we provide a result guaranteeing that if two datasets are related by $\varepsilon$-representativeness, i.e., both of them have points closer than $\varepsilon$, then the predictions by the classic decision tree are similar. Experimentally, we have also tested that $\varepsilon$-representativeness presents a significant correlation with the ordering of the feature importance. Moreover, we extend the results experimentally in the context of unseen vehicle collision data for XGboost, a machine-learning component widely adopted for dealing with tabular data.

SIMAP: A simplicial-map layer for neural networks

In this paper, we present SIMAP, a novel layer integrated into deep learning models, aimed at enhancing the interpretability of the output. The SIMAP layer is an enhanced version of Simplicial-Map Neural Networks (SMNNs), an explainable neural network based on support sets and simplicial maps (functions used in topology to transform shapes while preserving their structural connectivity). The novelty of the methodology proposed in this paper is two-fold: Firstly, SIMAP layers work in combination with other deep learning architectures as an interpretable layer substituting classic dense final layers. Secondly, unlike SMNNs, the support set is based on a fixed maximal simplex, the barycentric subdivision being efficiently computed with a matrix-based multiplication algorithm.

An In-Depth Analysis of Data Reduction Methods for Sustainable Deep Learning

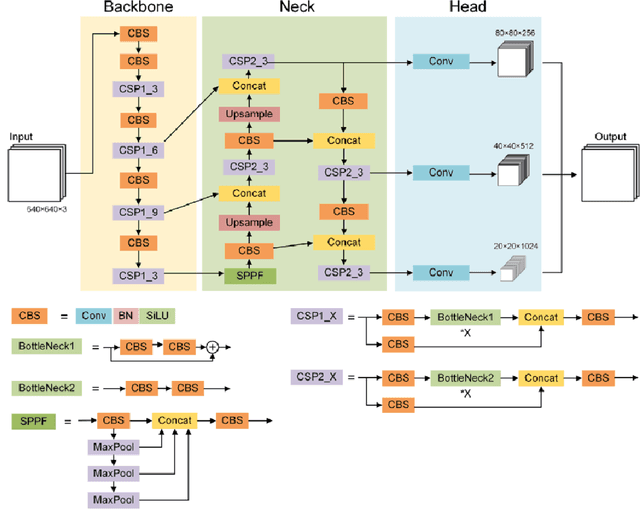
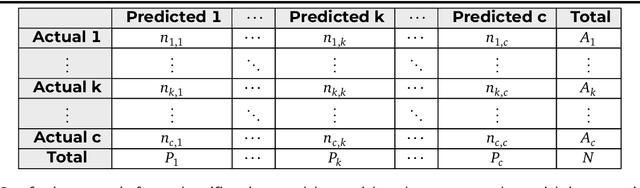
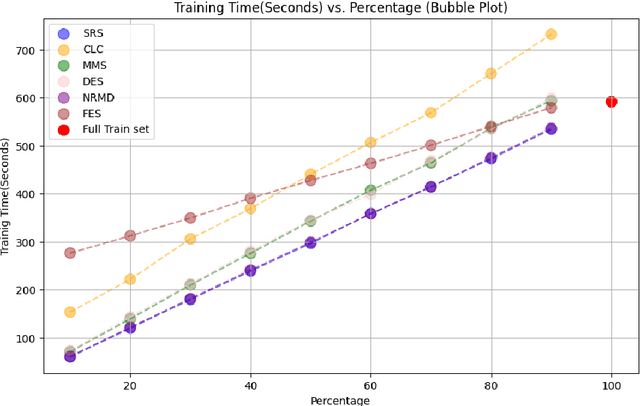
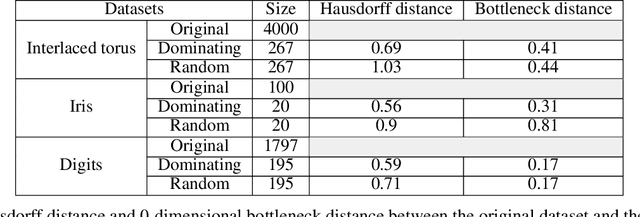
In recent years, Deep Learning has gained popularity for its ability to solve complex classification tasks, increasingly delivering better results thanks to the development of more accurate models, the availability of huge volumes of data and the improved computational capabilities of modern computers. However, these improvements in performance also bring efficiency problems, related to the storage of datasets and models, and to the waste of energy and time involved in both the training and inference processes. In this context, data reduction can help reduce energy consumption when training a deep learning model. In this paper, we present up to eight different methods to reduce the size of a tabular training dataset, and we develop a Python package to apply them. We also introduce a representativeness metric based on topology to measure how similar are the reduced datasets and the full training dataset. Additionally, we develop a methodology to apply these data reduction methods to image datasets for object detection tasks. Finally, we experimentally compare how these data reduction methods affect the representativeness of the reduced dataset, the energy consumption and the predictive performance of the model.

A Topological Approach to Measuring Training Data Quality

Data quality is crucial for the successful training, generalization and performance of artificial intelligence models. Furthermore, it is known that the leading approaches in artificial intelligence are notoriously data-hungry. In this paper, we propose the use of small training datasets towards faster training. Specifically, we provide a novel topological method based on morphisms between persistence modules to measure the training data quality with respect to the complete dataset. This way, we can provide an explanation of why the chosen training dataset will lead to poor performance.

Explainability in Simplicial Map Neural Networks

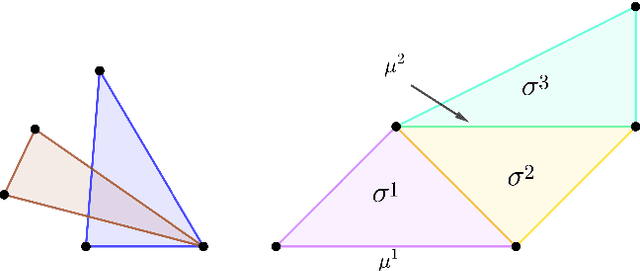
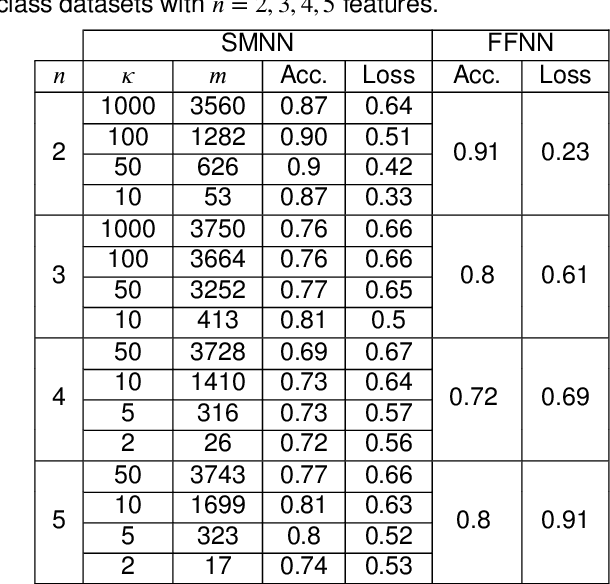
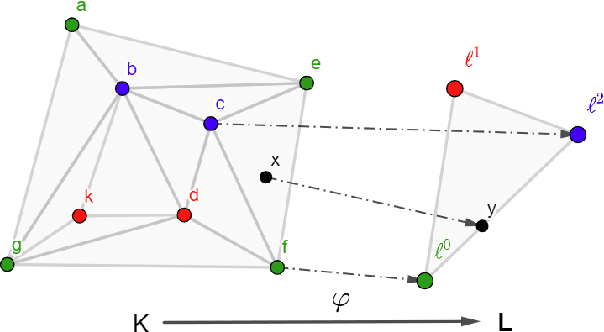
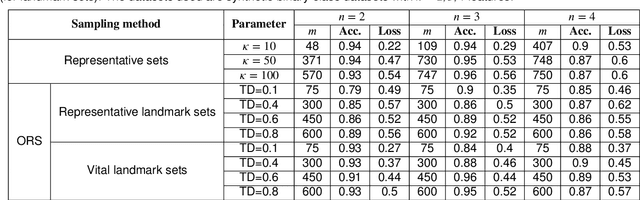
Simplicial map neural networks (SMNNs) are topology-based neural networks with interesting properties such as universal approximation capability and robustness to adversarial examples under appropriate conditions. However, SMNNs present some bottlenecks for their possible application in high dimensions. First, no SMNN training process has been defined so far. Second, SMNNs require the construction of a convex polytope surrounding the input dataset. In this paper, we propose a SMNN training procedure based on a support subset of the given dataset and a method based on projection to a hypersphere as a replacement for the convex polytope construction. In addition, the explainability capacity of SMNNs is also introduced for the first time in this paper.

Emotion recognition in talking-face videos using persistent entropy and neural networks

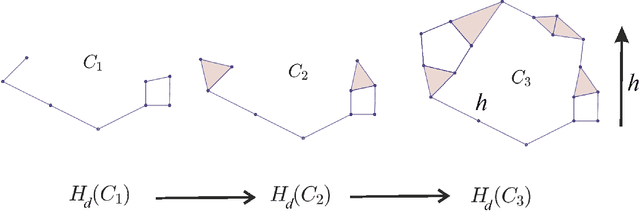
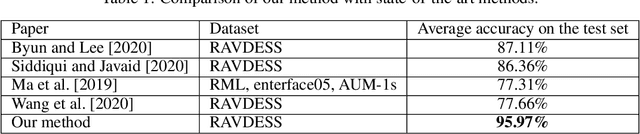
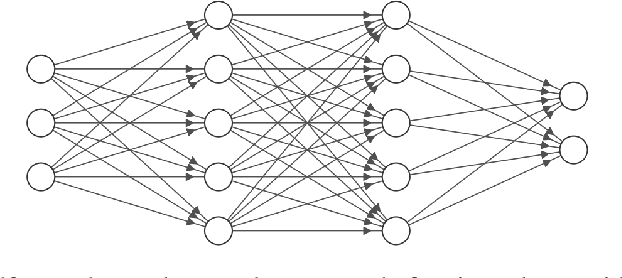
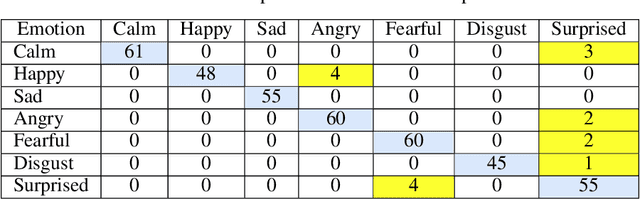
The automatic recognition of a person's emotional state has become a very active research field that involves scientists specialized in different areas such as artificial intelligence, computer vision or psychology, among others. Our main objective in this work is to develop a novel approach, using persistent entropy and neural networks as main tools, to recognise and classify emotions from talking-face videos. Specifically, we combine audio-signal and image-sequence information to compute a topology signature(a 9-dimensional vector) for each video. We prove that small changes in the video produce small changes in the signature. These topological signatures are used to feed a neural network to distinguish between the following emotions: neutral, calm, happy, sad, angry, fearful, disgust, and surprised. The results reached are promising and competitive, beating the performance reached in other state-of-the-art works found in the literature.

Towards a Philological Metric through a Topological Data Analysis Approach

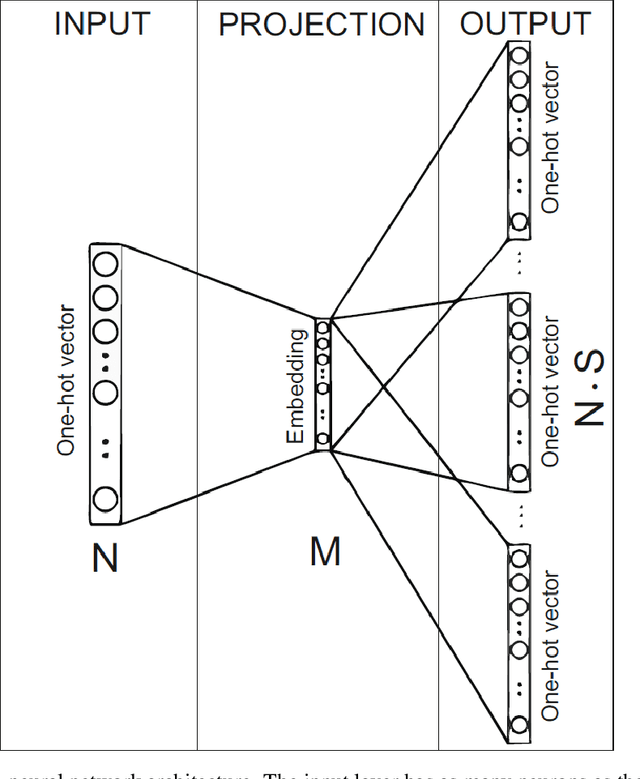
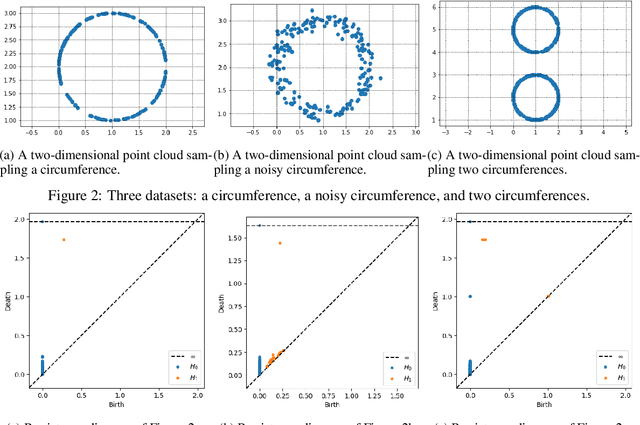
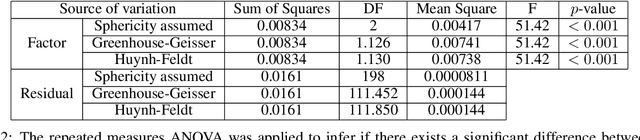
The canon of the baroque Spanish literature has been thoroughly studied with philological techniques. The major representatives of the poetry of this epoch are Francisco de Quevedo and Luis de G\'ongora y Argote. They are commonly classified by the literary experts in two different streams: Quevedo belongs to the Conceptismo and G\'ongora to the Culteranismo. Besides, traditionally, even if Quevedo is considered the most representative of the Conceptismo, Lope de Vega is also considered to be, at least, closely related to this literary trend. In this paper, we use Topological Data Analysis techniques to provide a first approach to a metric distance between the literary style of these poets. As a consequence, we reach results that are under the literary experts' criteria, locating the literary style of Lope de Vega, closer to the one of Quevedo than to the one of G\'ongora.

Two-hidden-layer Feedforward Neural Networks are Universal Approximators: A Constructive Approach

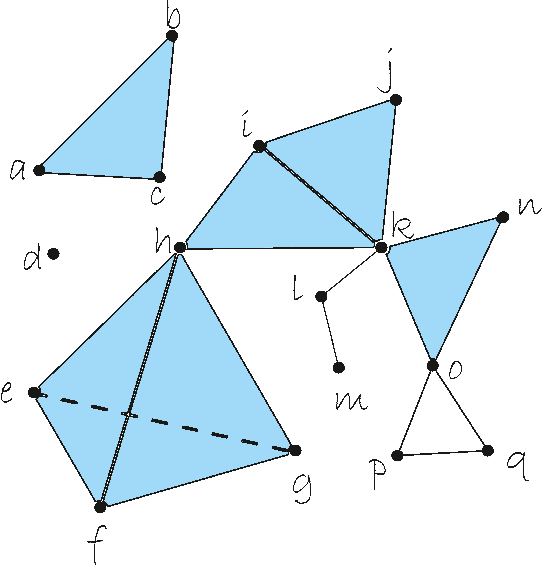
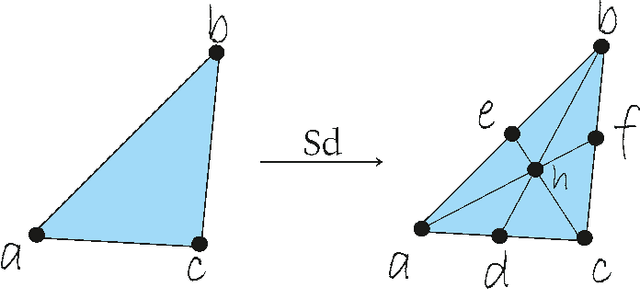
It is well known that Artificial Neural Networks are universal approximators. The classical result proves that, given a continuous function on a compact set on an n-dimensional space, then there exists a one-hidden-layer feedforward network which approximates the function. Such result proves the existence, but it does not provide a method for finding it. In this paper, a constructive approach to the proof of this property is given for the case of two-hidden-layer feedforward networks. This approach is based on an approximation of continuous functions by simplicial maps. Once a triangulation of the space is given, a concrete architecture and set of weights can be obtained. The quality of the approximation depends on the refinement of the covering of the space by simplicial complexes.

Representative Datasets: The Perceptron Case

One of the main drawbacks of the practical use of neural networks is the long time needed in the training process. Such training process consists in an iterative change of parameters trying to minimize a loss function. These changes are driven by a dataset, which can be seen as a set of labeled points in an n-dimensional space. In this paper, we explore the concept of it representative dataset which is smaller than the original dataset and satisfies a nearness condition independent of isometric transformations. The representativeness is measured using persistence diagrams due to its computational efficiency. We also prove that the accuracy of the learning process of a neural network on a representative dataset is comparable with the accuracy on the original dataset when the neural network architecture is a perceptron and the loss function is the mean squared error. These theoretical results accompanied with experimentation open a door to the size reduction of the dataset in order to gain time in the training process of any neural network.