Application of the representative measure approach to assess the reliability of decision trees in dealing with unseen vehicle collision data

Machine learning algorithms are fundamental components of novel data-informed Artificial Intelligence architecture. In this domain, the imperative role of representative datasets is a cornerstone in shaping the trajectory of artificial intelligence (AI) development. Representative datasets are needed to train machine learning components properly. Proper training has multiple impacts: it reduces the final model's complexity, power, and uncertainties. In this paper, we investigate the reliability of the $\varepsilon$-representativeness method to assess the dataset similarity from a theoretical perspective for decision trees. We decided to focus on the family of decision trees because it includes a wide variety of models known to be explainable. Thus, in this paper, we provide a result guaranteeing that if two datasets are related by $\varepsilon$-representativeness, i.e., both of them have points closer than $\varepsilon$, then the predictions by the classic decision tree are similar. Experimentally, we have also tested that $\varepsilon$-representativeness presents a significant correlation with the ordering of the feature importance. Moreover, we extend the results experimentally in the context of unseen vehicle collision data for XGboost, a machine-learning component widely adopted for dealing with tabular data.

An In-Depth Analysis of Data Reduction Methods for Sustainable Deep Learning

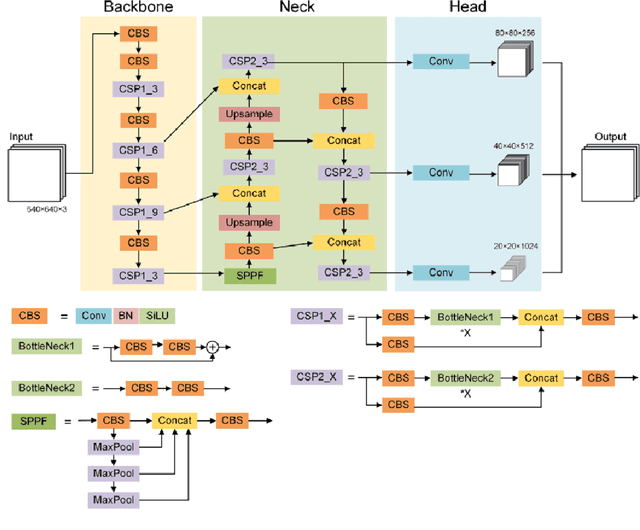
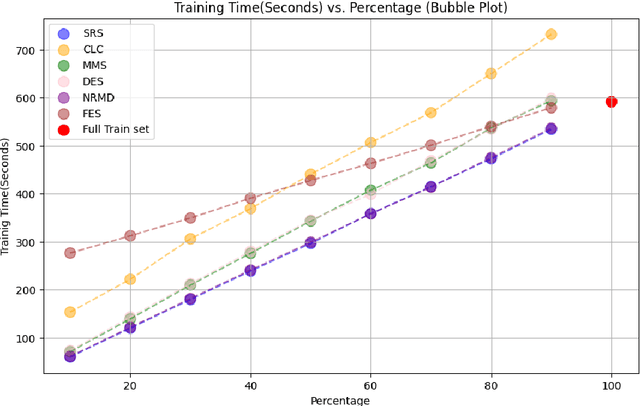
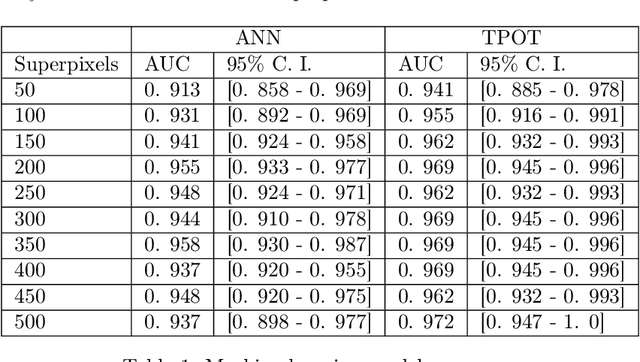
In recent years, Deep Learning has gained popularity for its ability to solve complex classification tasks, increasingly delivering better results thanks to the development of more accurate models, the availability of huge volumes of data and the improved computational capabilities of modern computers. However, these improvements in performance also bring efficiency problems, related to the storage of datasets and models, and to the waste of energy and time involved in both the training and inference processes. In this context, data reduction can help reduce energy consumption when training a deep learning model. In this paper, we present up to eight different methods to reduce the size of a tabular training dataset, and we develop a Python package to apply them. We also introduce a representativeness metric based on topology to measure how similar are the reduced datasets and the full training dataset. Additionally, we develop a methodology to apply these data reduction methods to image datasets for object detection tasks. Finally, we experimentally compare how these data reduction methods affect the representativeness of the reduced dataset, the energy consumption and the predictive performance of the model.

Fast Glioblastoma Detection in Fluid-attenuated inversion recovery (FLAIR) images by Topological Explainable Automatic Machine Learning

Glioblastoma multiforme (GBM) is a fast-growing and highly invasive brain tumor, it tends to occur in adults between the ages of 45 and 70 and it accounts for 52 percent of all primary brain tumors. Usually, GBMs are detected by magnetic resonance images (MRI). Among MRI images, Fluid-attenuated inversion recovery (FLAIR) sequence produces high quality digital tumor representation. Fast detection and segmentation techniques are needed for overcoming subjective medical doctors (MDs) judgment. In this work, a new framework for radiomics analysis of GBM on FLAIR images is proposed. The framework can be used both for an initial detection of GBM and in case for its segmentation. The novelty of the methodology is the combination of new topological features computed by topological data analysis, textural features and of automatic interpretable machine learning algorithm. The framework was evaluated on a public available dataset and it reaches up to the 97% of accuracy on the detection task and up to 95% of accuracy on the segmentation task.

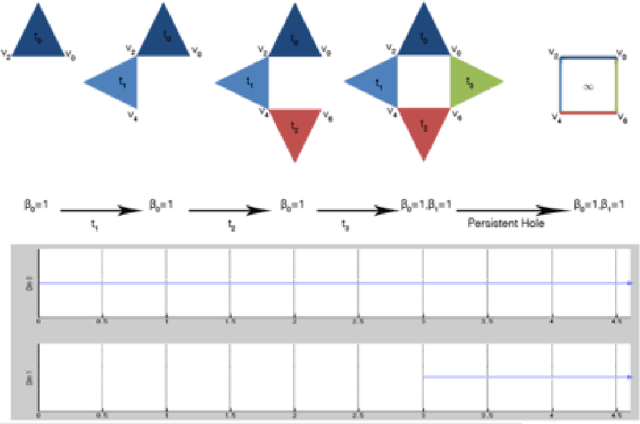
Neural Hypernetwork Approach for Pulmonary Embolism diagnosis

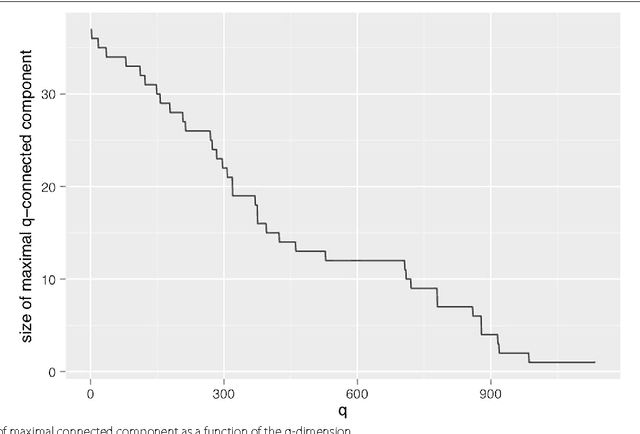
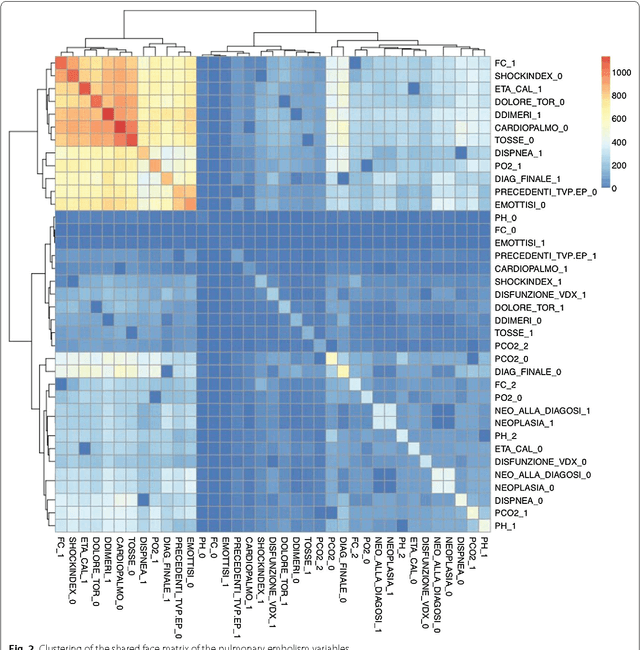
This work introduces an integrative approach based on Q-analysis with machine learning. The new approach, called Neural Hypernetwork, has been applied to a case study of pulmonary embolism diagnosis. The objective of the application of neural hyper-network to pulmonary embolism (PE) is to improve diagnose for reducing the number of CT-angiography needed. Hypernetworks, based on topological simplicial complex, generalize the concept of two-relation to many-body relation. Furthermore, Hypernetworks provide a significant generalization of network theory, enabling the integration of relational structure, logic and analytic dynamics. Another important results is that Q-analysis stays close to the data, while other approaches manipulate data, projecting them into metric spaces or applying some filtering functions to highlight the intrinsic relations. A pulmonary embolism (PE) is a blockage of the main artery of the lung or one of its branches, frequently fatal. Our study uses data on 28 diagnostic features of 1,427 people considered to be at risk of PE. The resulting neural hypernetwork correctly recognized 94% of those developing a PE. This is better than previous results that have been obtained with other methods (statistical selection of features, partial least squares regression, topological data analysis in a metric space).