Two-hidden-layer Feedforward Neural Networks are Universal Approximators: A Constructive Approach
Paper and Code
Jul 26, 2019
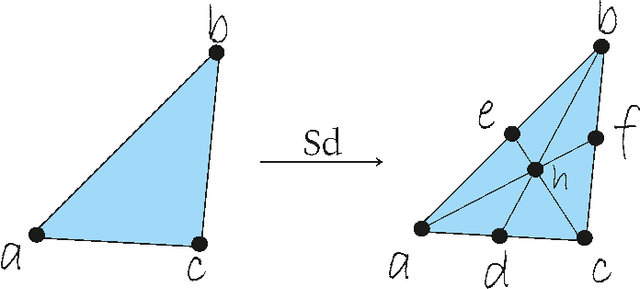
It is well known that Artificial Neural Networks are universal approximators. The classical result proves that, given a continuous function on a compact set on an n-dimensional space, then there exists a one-hidden-layer feedforward network which approximates the function. Such result proves the existence, but it does not provide a method for finding it. In this paper, a constructive approach to the proof of this property is given for the case of two-hidden-layer feedforward networks. This approach is based on an approximation of continuous functions by simplicial maps. Once a triangulation of the space is given, a concrete architecture and set of weights can be obtained. The quality of the approximation depends on the refinement of the covering of the space by simplicial complexes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge