Prediction and outlier detection: a distribution-free prediction set with a balanced objective

We consider the multi-class classification problem when the training data and the out-of-sample test data may have different distributions and propose a method called BCOPS (balanced and conformal optimized prediction set) that constructs a prediction set C(x) which tries to optimize out-of-sample performance, aiming to include the correct class as often as possible, but also detecting outliers x, for which the method returns no prediction (corresponding to C(x) equal to the empty set). BCOPS combines supervised-learning algorithms with the method of conformal prediction to minimize a misclassification loss averaged over the out-of-sample distribution. The constructed prediction sets have a finite-sample coverage guarantee without distributional assumptions. We also develop a variant of BCOPS in the online setting where we optimize the misclassification loss averaged over a proxy of the out-of-sample distribution. We also describe new methods for the evaluation of out-of-sample performance with mismatched data. We prove asymptotic consistency and efficiency of the proposed methods under suitable assumptions and illustrate our methods on real data examples.

Discriminant Analysis with Adaptively Pooled Covariance

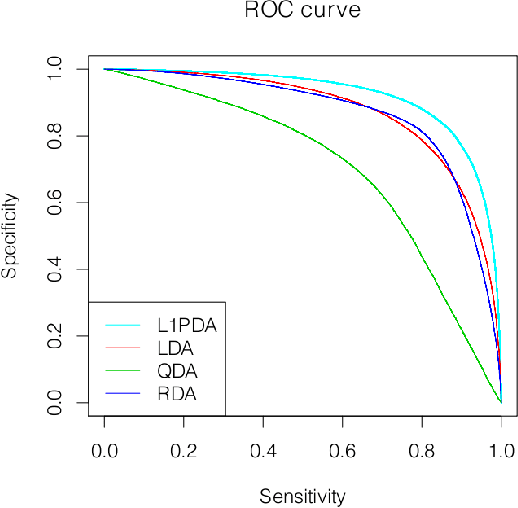
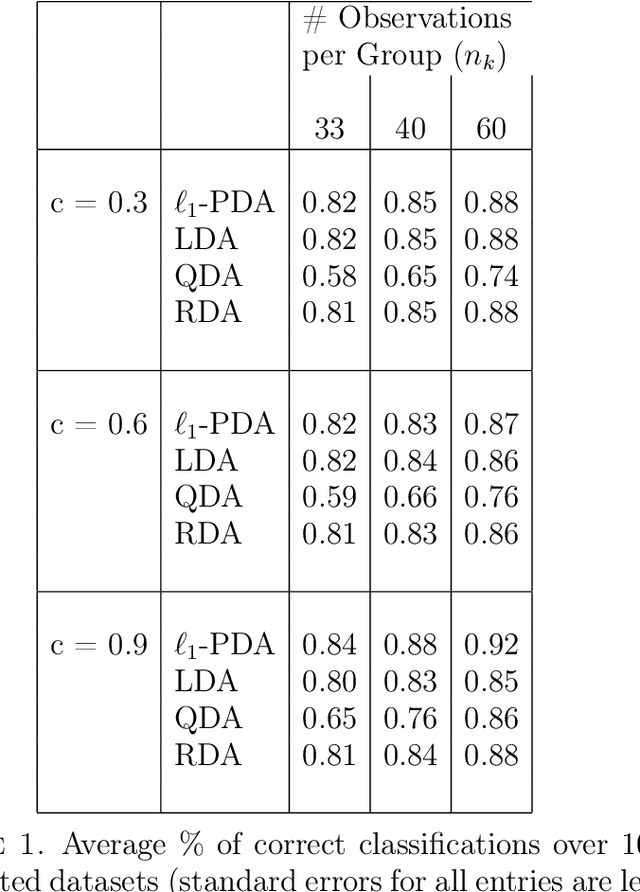
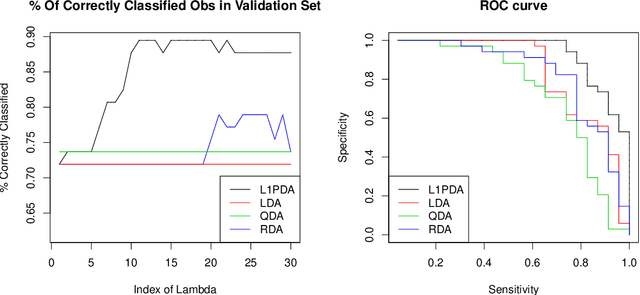
Linear and Quadratic Discriminant analysis (LDA/QDA) are common tools for classification problems. For these methods we assume observations are normally distributed within group. We estimate a mean and covariance matrix for each group and classify using Bayes theorem. With LDA, we estimate a single, pooled covariance matrix, while for QDA we estimate a separate covariance matrix for each group. Rarely do we believe in a homogeneous covariance structure between groups, but often there is insufficient data to separately estimate covariance matrices. We propose L1- PDA, a regularized model which adaptively pools elements of the precision matrices. Adaptively pooling these matrices decreases the variance of our estimates (as in LDA), without overly biasing them. In this paper, we propose and discuss this method, give an efficient algorithm to fit it for moderate sized problems, and show its efficacy on real and simulated datasets.

Regularization methods for learning incomplete matrices

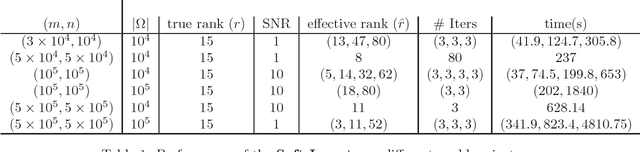
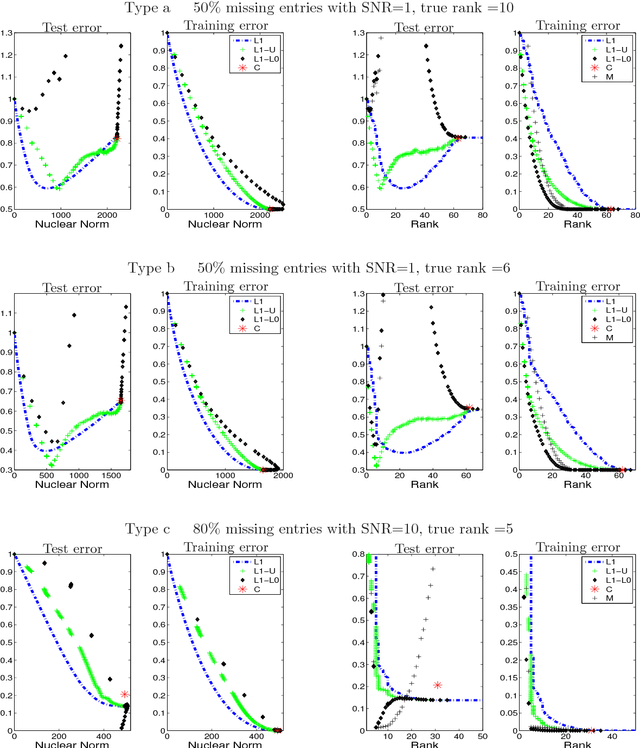
We use convex relaxation techniques to provide a sequence of solutions to the matrix completion problem. Using the nuclear norm as a regularizer, we provide simple and very efficient algorithms for minimizing the reconstruction error subject to a bound on the nuclear norm. Our algorithm iteratively replaces the missing elements with those obtained from a thresholded SVD. With warm starts this allows us to efficiently compute an entire regularization path of solutions.