Regularization methods for learning incomplete matrices
Paper and Code
Jun 11, 2009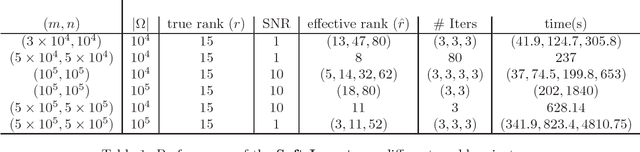
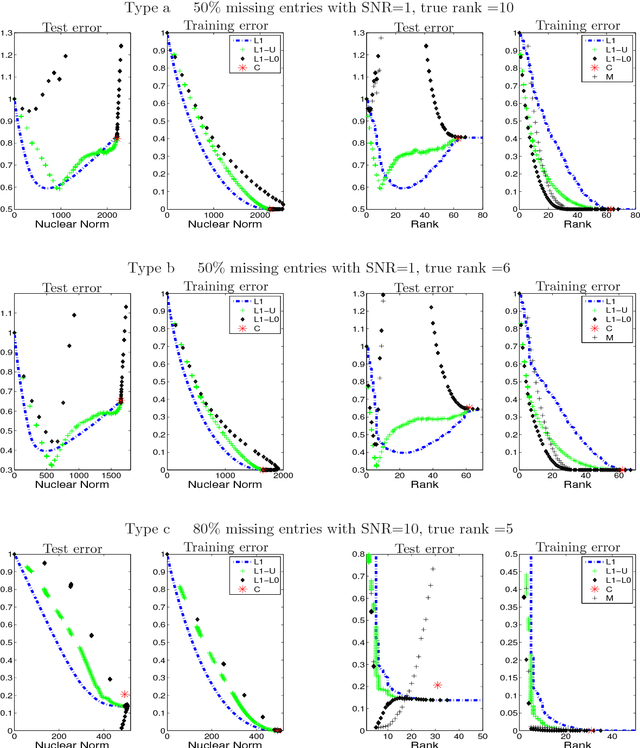
We use convex relaxation techniques to provide a sequence of solutions to the matrix completion problem. Using the nuclear norm as a regularizer, we provide simple and very efficient algorithms for minimizing the reconstruction error subject to a bound on the nuclear norm. Our algorithm iteratively replaces the missing elements with those obtained from a thresholded SVD. With warm starts this allows us to efficiently compute an entire regularization path of solutions.
* 10 pages, 1 figure
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge