Discriminant Analysis with Adaptively Pooled Covariance
Paper and Code
Dec 06, 2011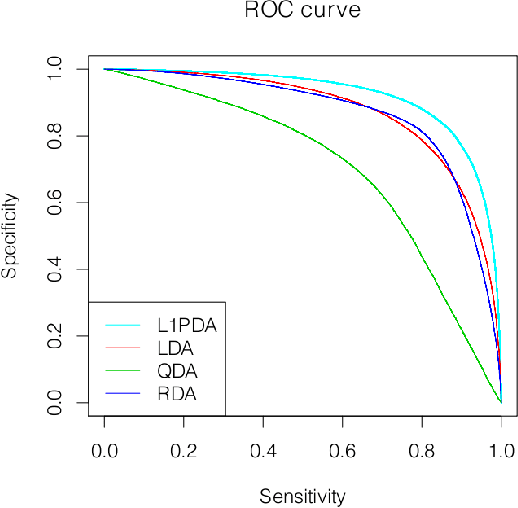
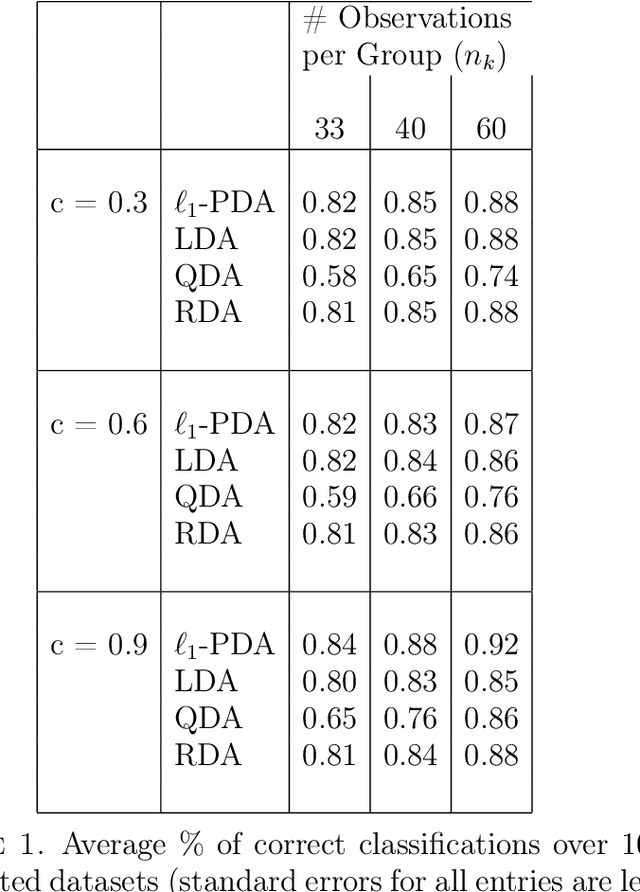
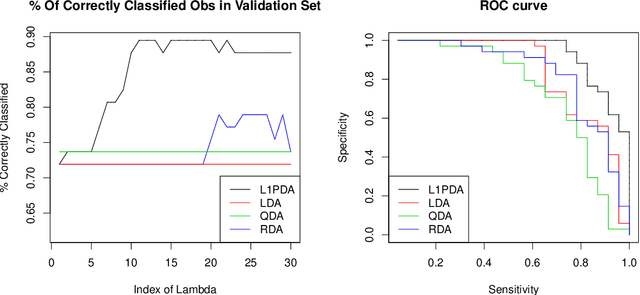
Linear and Quadratic Discriminant analysis (LDA/QDA) are common tools for classification problems. For these methods we assume observations are normally distributed within group. We estimate a mean and covariance matrix for each group and classify using Bayes theorem. With LDA, we estimate a single, pooled covariance matrix, while for QDA we estimate a separate covariance matrix for each group. Rarely do we believe in a homogeneous covariance structure between groups, but often there is insufficient data to separately estimate covariance matrices. We propose L1- PDA, a regularized model which adaptively pools elements of the precision matrices. Adaptively pooling these matrices decreases the variance of our estimates (as in LDA), without overly biasing them. In this paper, we propose and discuss this method, give an efficient algorithm to fit it for moderate sized problems, and show its efficacy on real and simulated datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge