Ad Hoc Microphone Array Calibration: Euclidean Distance Matrix Completion Algorithm and Theoretical Guarantees

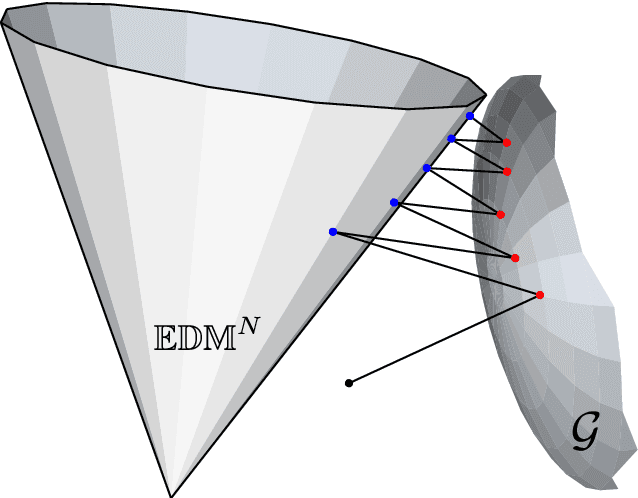
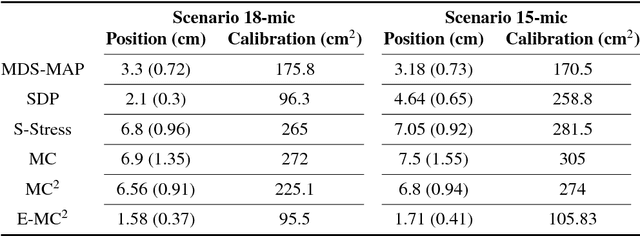
This paper addresses the problem of ad hoc microphone array calibration where only partial information about the distances between microphones is available. We construct a matrix consisting of the pairwise distances and propose to estimate the missing entries based on a novel Euclidean distance matrix completion algorithm by alternative low-rank matrix completion and projection onto the Euclidean distance space. This approach confines the recovered matrix to the EDM cone at each iteration of the matrix completion algorithm. The theoretical guarantees of the calibration performance are obtained considering the random and locally structured missing entries as well as the measurement noise on the known distances. This study elucidates the links between the calibration error and the number of microphones along with the noise level and the ratio of missing distances. Thorough experiments on real data recordings and simulated setups are conducted to demonstrate these theoretical insights. A significant improvement is achieved by the proposed Euclidean distance matrix completion algorithm over the state-of-the-art techniques for ad hoc microphone array calibration.

Calibration Using Matrix Completion with Application to Ultrasound Tomography

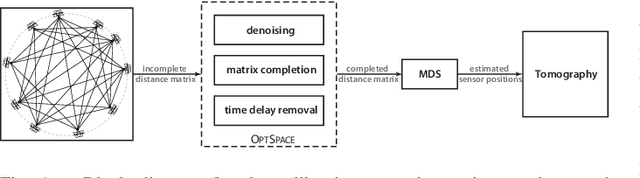
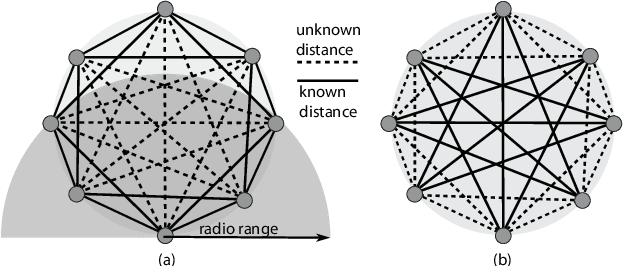
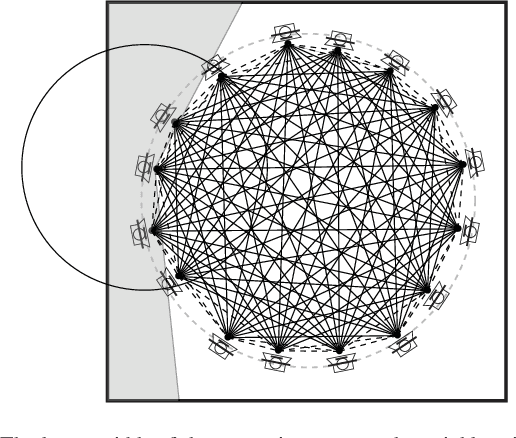
We study the calibration process in circular ultrasound tomography devices where the sensor positions deviate from the circumference of a perfect circle. This problem arises in a variety of applications in signal processing ranging from breast imaging to sensor network localization. We introduce a novel method of calibration/localization based on the time-of-flight (ToF) measurements between sensors when the enclosed medium is homogeneous. In the presence of all the pairwise ToFs, one can easily estimate the sensor positions using multi-dimensional scaling (MDS) method. In practice however, due to the transitional behaviour of the sensors and the beam form of the transducers, the ToF measurements for close-by sensors are unavailable. Further, random malfunctioning of the sensors leads to random missing ToF measurements. On top of the missing entries, in practice an unknown time delay is also added to the measurements. In this work, we incorporate the fact that a matrix defined from all the ToF measurements is of rank at most four. In order to estimate the missing ToFs, we apply a state-of-the-art low-rank matrix completion algorithm, OPTSPACE . To find the correct positions of the sensors (our ultimate goal) we then apply MDS. We show analytic bounds on the overall error of the whole process in the presence of noise and hence deduce its robustness. Finally, we confirm the functionality of our method in practice by simulations mimicking the measurements of a circular ultrasound tomography device.