Low-rank and Sparse Soft Targets to Learn Better DNN Acoustic Models

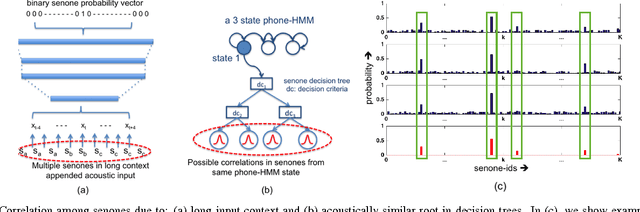
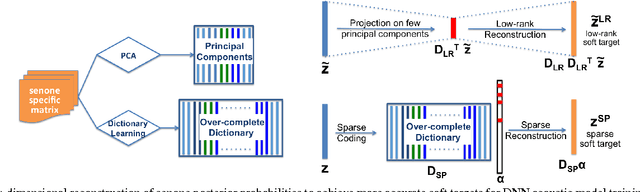
Conventional deep neural networks (DNN) for speech acoustic modeling rely on Gaussian mixture models (GMM) and hidden Markov model (HMM) to obtain binary class labels as the targets for DNN training. Subword classes in speech recognition systems correspond to context-dependent tied states or senones. The present work addresses some limitations of GMM-HMM senone alignments for DNN training. We hypothesize that the senone probabilities obtained from a DNN trained with binary labels can provide more accurate targets to learn better acoustic models. However, DNN outputs bear inaccuracies which are exhibited as high dimensional unstructured noise, whereas the informative components are structured and low-dimensional. We exploit principle component analysis (PCA) and sparse coding to characterize the senone subspaces. Enhanced probabilities obtained from low-rank and sparse reconstructions are used as soft-targets for DNN acoustic modeling, that also enables training with untranscribed data. Experiments conducted on AMI corpus shows 4.6% relative reduction in word error rate.

Exploiting Low-dimensional Structures to Enhance DNN Based Acoustic Modeling in Speech Recognition

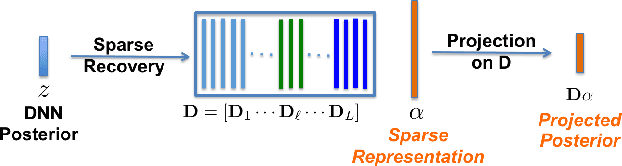
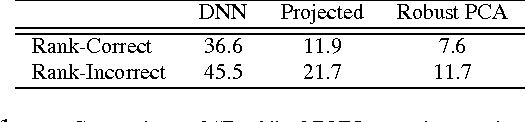
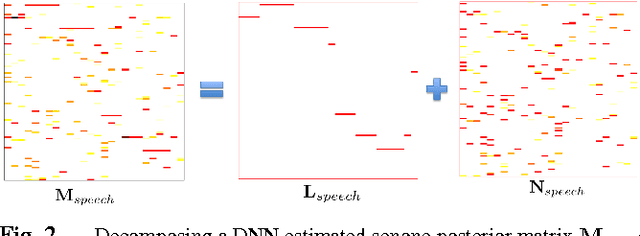
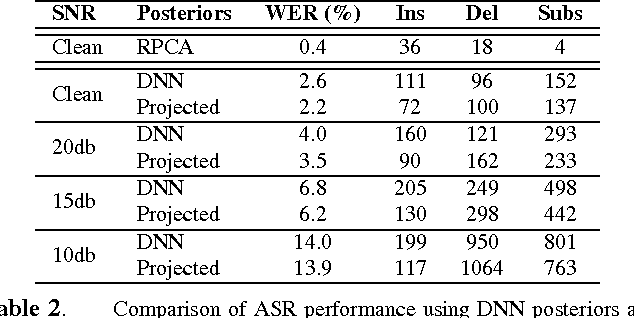
We propose to model the acoustic space of deep neural network (DNN) class-conditional posterior probabilities as a union of low-dimensional subspaces. To that end, the training posteriors are used for dictionary learning and sparse coding. Sparse representation of the test posteriors using this dictionary enables projection to the space of training data. Relying on the fact that the intrinsic dimensions of the posterior subspaces are indeed very small and the matrix of all posteriors belonging to a class has a very low rank, we demonstrate how low-dimensional structures enable further enhancement of the posteriors and rectify the spurious errors due to mismatch conditions. The enhanced acoustic modeling method leads to improvements in continuous speech recognition task using hybrid DNN-HMM (hidden Markov model) framework in both clean and noisy conditions, where upto 15.4% relative reduction in word error rate (WER) is achieved.

Ad Hoc Microphone Array Calibration: Euclidean Distance Matrix Completion Algorithm and Theoretical Guarantees

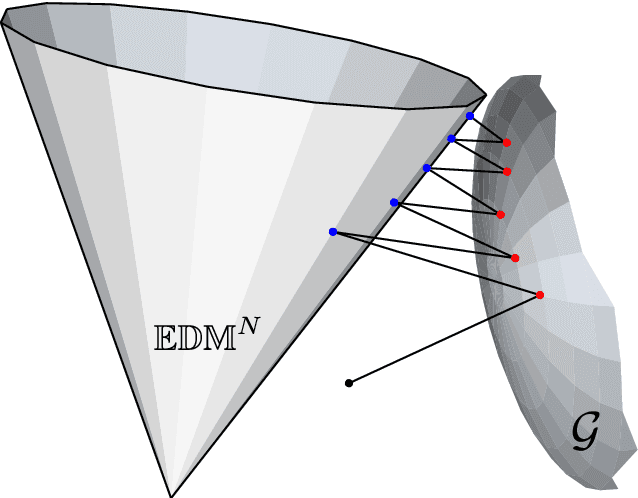
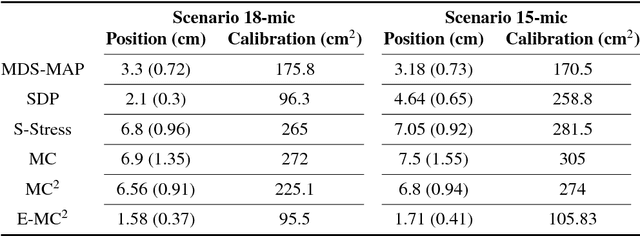
This paper addresses the problem of ad hoc microphone array calibration where only partial information about the distances between microphones is available. We construct a matrix consisting of the pairwise distances and propose to estimate the missing entries based on a novel Euclidean distance matrix completion algorithm by alternative low-rank matrix completion and projection onto the Euclidean distance space. This approach confines the recovered matrix to the EDM cone at each iteration of the matrix completion algorithm. The theoretical guarantees of the calibration performance are obtained considering the random and locally structured missing entries as well as the measurement noise on the known distances. This study elucidates the links between the calibration error and the number of microphones along with the noise level and the ratio of missing distances. Thorough experiments on real data recordings and simulated setups are conducted to demonstrate these theoretical insights. A significant improvement is achieved by the proposed Euclidean distance matrix completion algorithm over the state-of-the-art techniques for ad hoc microphone array calibration.