A Debate-Driven Experiment on LLM Hallucinations and Accuracy

Large language models (LLMs) have achieved a degree of success in generating coherent and contextually relevant text, yet they remain prone to a significant challenge known as hallucination: producing information that is not substantiated by the input or external knowledge. Previous efforts to mitigate hallucinations have focused on techniques such as fine-tuning models on high-quality datasets, incorporating fact-checking mechanisms, and developing adversarial training methods. While these approaches have shown some promise, they often address the issue at the level of individual model outputs, leaving unexplored the effects of inter-model interactions on hallucination. This study investigates the phenomenon of hallucination in LLMs through a novel experimental framework where multiple instances of GPT-4o-Mini models engage in a debate-like interaction prompted with questions from the TruthfulQA dataset. One model is deliberately instructed to generate plausible but false answers while the other models are asked to respond truthfully. The experiment is designed to assess whether the introduction of misinformation by one model can challenge the truthful majority to better justify their reasoning, improving performance on the TruthfulQA benchmark. The findings suggest that inter-model interactions can offer valuable insights into improving the accuracy and robustness of LLM outputs, complementing existing mitigation strategies.

CopyCat2: A Single Model for Multi-Speaker TTS and Many-to-Many Fine-Grained Prosody Transfer

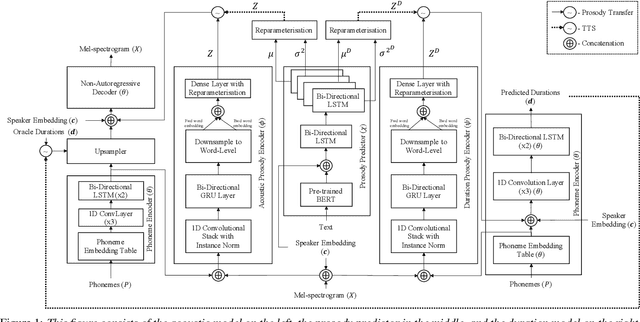
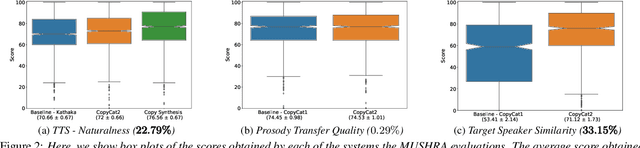
In this paper, we present CopyCat2 (CC2), a novel model capable of: a) synthesizing speech with different speaker identities, b) generating speech with expressive and contextually appropriate prosody, and c) transferring prosody at fine-grained level between any pair of seen speakers. We do this by activating distinct parts of the network for different tasks. We train our model using a novel approach to two-stage training. In Stage I, the model learns speaker-independent word-level prosody representations from speech which it uses for many-to-many fine-grained prosody transfer. In Stage II, we learn to predict these prosody representations using the contextual information available in text, thereby, enabling multi-speaker TTS with contextually appropriate prosody. We compare CC2 to two strong baselines, one in TTS with contextually appropriate prosody, and one in fine-grained prosody transfer. CC2 reduces the gap in naturalness between our baseline and copy-synthesised speech by $22.79\%$. In fine-grained prosody transfer evaluations, it obtains a relative improvement of $33.15\%$ in target speaker similarity.

A Tight Analysis of Greedy Yields Subexponential Time Approximation for Uniform Decision Tree

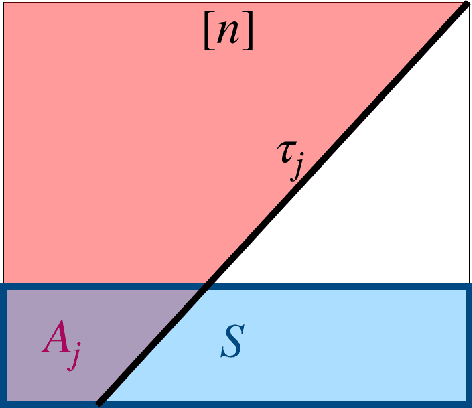
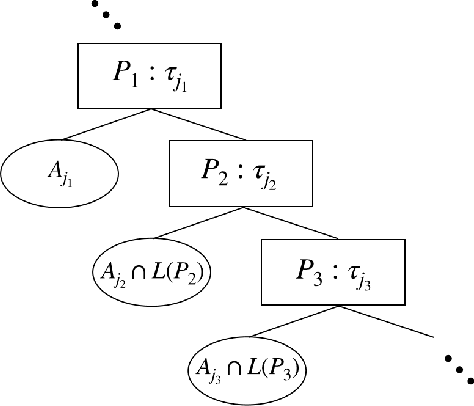
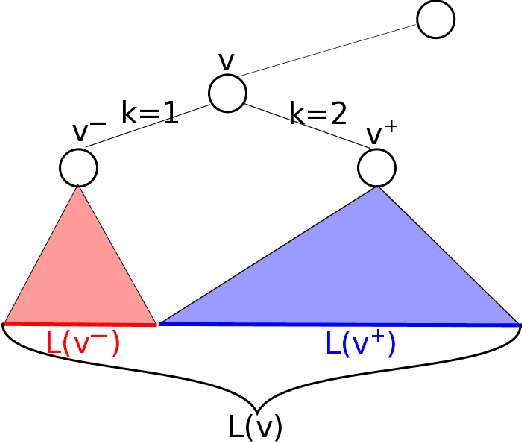
Decision Tree is a classic formulation of active learning: given $n$ hypotheses with nonnegative weights summing to 1 and a set of tests that each partition the hypotheses, output a decision tree using the provided tests that uniquely identifies each hypothesis and has minimum (weighted) average depth. Previous works showed that the greedy algorithm achieves a $O(\log n)$ approximation ratio for this problem and it is NP-hard beat a $O(\log n)$ approximation, settling the complexity of the problem. However, for Uniform Decision Tree, i.e. Decision Tree with uniform weights, the story is more subtle. The greedy algorithm's $O(\log n)$ approximation ratio is the best known, but the largest approximation ratio known to be NP-hard is $4-\varepsilon$. We prove that the greedy algorithm gives a $O(\frac{\log n}{\log C_{OPT}})$ approximation for Uniform Decision Tree, where $C_{OPT}$ is the cost of the optimal tree and show this is best possible for the greedy algorithm. As a corollary, this resolves a conjecture of Kosaraju, Przytycka, and Borgstrom. Our results also hold for instances of Decision Tree whose weights are not too far from uniform. Leveraging this result, we exhibit a subexponential algorithm that yields an $O(1/\alpha)$ approximation to Uniform Decision Tree in time $2^{O(n^\alpha)}$. As a corollary, achieving any super-constant approximation ratio on Uniform Decision Tree is not NP-hard, assuming the Exponential Time Hypothesis. This work therefore adds approximating Uniform Decision Tree to a small list of natural problems that have subexponential algorithms but no known polynomial time algorithms. Like the greedy algorithm, our subexponential algorithm gives similar guarantees even for slightly nonuniform weights.