A Tight Analysis of Greedy Yields Subexponential Time Approximation for Uniform Decision Tree

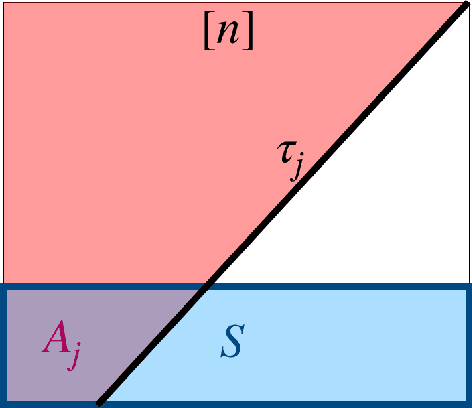
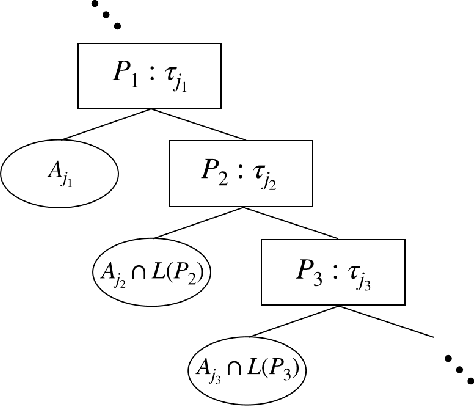
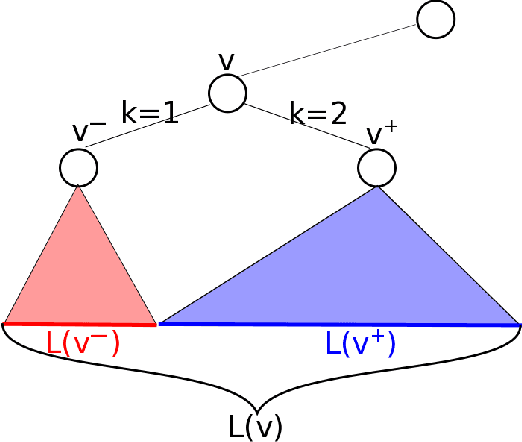
Decision Tree is a classic formulation of active learning: given $n$ hypotheses with nonnegative weights summing to 1 and a set of tests that each partition the hypotheses, output a decision tree using the provided tests that uniquely identifies each hypothesis and has minimum (weighted) average depth. Previous works showed that the greedy algorithm achieves a $O(\log n)$ approximation ratio for this problem and it is NP-hard beat a $O(\log n)$ approximation, settling the complexity of the problem. However, for Uniform Decision Tree, i.e. Decision Tree with uniform weights, the story is more subtle. The greedy algorithm's $O(\log n)$ approximation ratio is the best known, but the largest approximation ratio known to be NP-hard is $4-\varepsilon$. We prove that the greedy algorithm gives a $O(\frac{\log n}{\log C_{OPT}})$ approximation for Uniform Decision Tree, where $C_{OPT}$ is the cost of the optimal tree and show this is best possible for the greedy algorithm. As a corollary, this resolves a conjecture of Kosaraju, Przytycka, and Borgstrom. Our results also hold for instances of Decision Tree whose weights are not too far from uniform. Leveraging this result, we exhibit a subexponential algorithm that yields an $O(1/\alpha)$ approximation to Uniform Decision Tree in time $2^{O(n^\alpha)}$. As a corollary, achieving any super-constant approximation ratio on Uniform Decision Tree is not NP-hard, assuming the Exponential Time Hypothesis. This work therefore adds approximating Uniform Decision Tree to a small list of natural problems that have subexponential algorithms but no known polynomial time algorithms. Like the greedy algorithm, our subexponential algorithm gives similar guarantees even for slightly nonuniform weights.