Iterative Refinement Diffusion for Super-Resolved Data Assimilation of Multiscale Physical Systems

Recovering high-resolution states from sparse, low-resolution observations is a central challenge in scientific machine learning and data assimilation. Classical data assimilation exploits temporal information through forecast-analysis cycles, but often requires repeated access to expensive high-resolution forecast models. Generative super-resolution can recover unresolved structure from coarse observations, but is commonly used as a one-shot mapping that does not fully exploit constraints from past states. We introduce Iterative Refinement (IR), a learned data assimilation framework that combines these perspectives. Instead of performing a single coarse-to-fine reconstruction, IR decomposes the task into resolution-wise forecast-analysis operations across a multiresolution hierarchy. At each stage, a shared neural operator with resolution-dependent spectral mode slicing provides a dynamical prior, while a shared conditional diffusion corrector uses the current coarser-resolution state to produce a refined posterior at the next finer resolution. We evaluate IR on one-dimensional stochastically forced Burgers dynamics and two-dimensional Kraichnan turbulence. On the challenging 256x256 Kraichnan benchmark, IR achieves an RMSE of 0.184 and an SSIM of 0.836, outperforming spectral upsampling, one-shot diffusion super-resolution, enhanced deep super-resolution, and an autoregressive forecaster. On the more constrained Burgers testbed, IR remains competitive with one-shot diffusion, which achieves the lowest RMSE. These results show that one-shot generative reconstruction can be effective for simpler settings, while hierarchical forecast-analysis refinement becomes advantageous in strongly multiscale and underdetermined regimes. Overall, IR combines temporal priors, generative correction, and multiresolution reconstruction for learned data assimilation in complex physical systems.

Diffusion models recover accurate mixture weights despite score function insensitivity

Score-based generative models exhibit a puzzling behavior: they often appear to cover all modes of a target multimodal distribution and yet may fail to learn the correct relative mode amplitudes, which can be interpreted as mixture weights. We resolve this apparent paradox by relating the diffusion score matching (DSM) loss to the error in estimating mixture weights from generated samples. We show that, even when the target score is insensitive to mixture weights, generated samples can recover the weights accurately if the scores at intermediate noise levels are informative about the weights. Accordingly, we define the diffusion score sensitivity index (DSSI) as the variation in the DSM loss relative to changes in a parameter. We then show that the DSSI governs the accuracy with which the parameter of the target distribution can be estimated from generated samples. For Gaussian mixtures in arbitrary dimensions, we prove that the mixture weight estimation errors are on the same order as the DSM loss under mild conditions. Empirically, we show the emergence of sensitivity during the noising process of benchmark data distributions under typical noise schedules, and that these sensitivity values predict how well a well-trained model recovers mixture weights. Furthermore, we show that the choice of noise schedule can reduce diffusion sensitivity, leading to mode amplification. Although we focus on mixture weights, the proposed sensitivity framework governs the recovery of any qualitative parameter of the target distribution.

Disentangling Safe and Unsafe Corruptions via Anisotropy and Locality

State-of-the-art machine learning systems are vulnerable to small perturbations to their input, where ``small'' is defined according to a threat model that assigns a positive threat to each perturbation. Most prior works define a task-agnostic, isotropic, and global threat, like the $\ell_p$ norm, where the magnitude of the perturbation fully determines the degree of the threat and neither the direction of the attack nor its position in space matter. However, common corruptions in computer vision, such as blur, compression, or occlusions, are not well captured by such threat models. This paper proposes a novel threat model called \texttt{Projected Displacement} (PD) to study robustness beyond existing isotropic and global threat models. The proposed threat model measures the threat of a perturbation via its alignment with \textit{unsafe directions}, defined as directions in the input space along which a perturbation of sufficient magnitude changes the ground truth class label. Unsafe directions are identified locally for each input based on observed training data. In this way, the PD threat model exhibits anisotropy and locality. Experiments on Imagenet-1k data indicate that, for any input, the set of perturbations with small PD threat includes \textit{safe} perturbations of large $\ell_p$ norm that preserve the true label, such as noise, blur and compression, while simultaneously excluding \textit{unsafe} perturbations that alter the true label. Unlike perceptual threat models based on embeddings of large-vision models, the PD threat model can be readily computed for arbitrary classification tasks without pre-training or finetuning. Further additional task annotation such as sensitivity to image regions or concept hierarchies can be easily integrated into the assessment of threat and thus the PD threat model presents practitioners with a flexible, task-driven threat specification.

Sparsity-aware generalization theory for deep neural networks

Deep artificial neural networks achieve surprising generalization abilities that remain poorly understood. In this paper, we present a new approach to analyzing generalization for deep feed-forward ReLU networks that takes advantage of the degree of sparsity that is achieved in the hidden layer activations. By developing a framework that accounts for this reduced effective model size for each input sample, we are able to show fundamental trade-offs between sparsity and generalization. Importantly, our results make no strong assumptions about the degree of sparsity achieved by the model, and it improves over recent norm-based approaches. We illustrate our results numerically, demonstrating non-vacuous bounds when coupled with data-dependent priors in specific settings, even in over-parametrized models.

Adversarial robustness of sparse local Lipschitz predictors

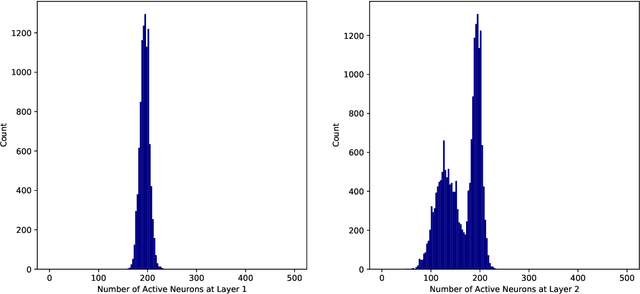
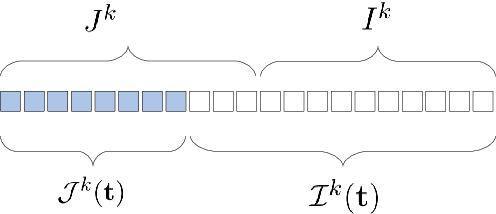
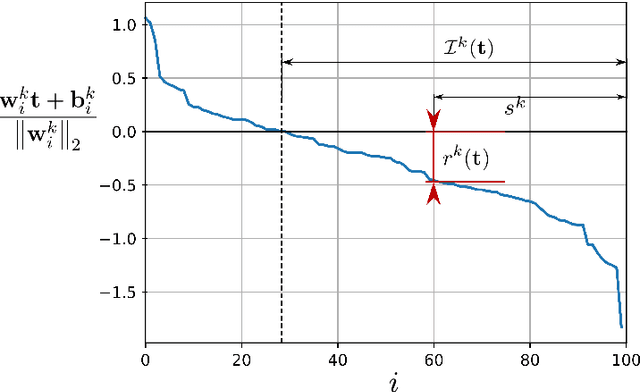
This work studies the adversarial robustness of parametric functions composed of a linear predictor and a non-linear representation map. Our analysis relies on sparse local Lipschitzness (SLL), an extension of local Lipschitz continuity that better captures the stability and reduced effective dimensionality of predictors upon local perturbations. SLL functions preserve a certain degree of structure, given by the sparsity pattern in the representation map, and include several popular hypothesis classes, such as piece-wise linear models, Lasso and its variants, and deep feed-forward ReLU networks. We provide a tighter robustness certificate on the minimal energy of an adversarial example, as well as tighter data-dependent non-uniform bounds on the robust generalization error of these predictors. We instantiate these results for the case of deep neural networks and provide numerical evidence that supports our results, shedding new insights into natural regularization strategies to increase the robustness of these models.

A Study of Neural Training with Non-Gradient and Noise Assisted Gradient Methods

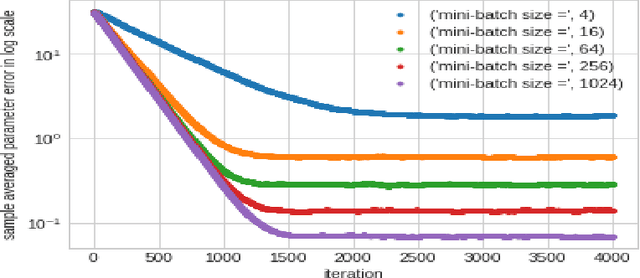
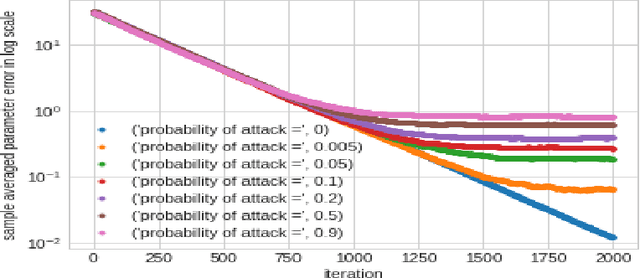
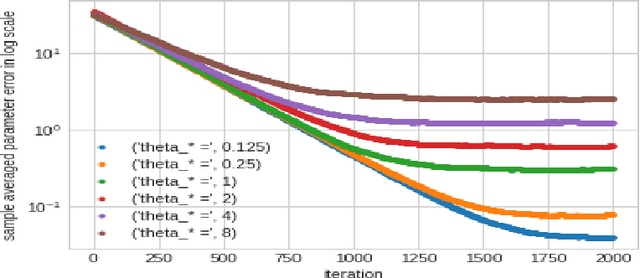
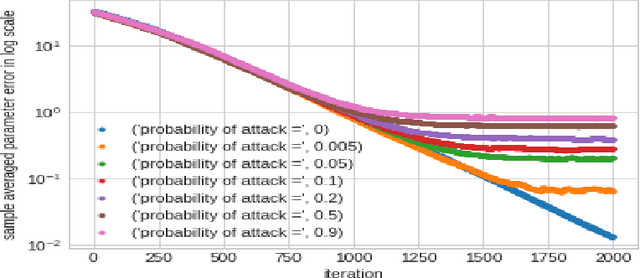
In this work we demonstrate provable guarantees on the training of depth-2 neural networks in new regimes than previously explored. (1) We start with a simple stochastic algorithm that can train a ReLU gate in the realizable setting with significantly milder conditions on the data distribution than previous results. Leveraging some additional distributional assumptions we also show near-optimal guarantees of training a ReLU gate when an adversary is allowed to corrupt the true labels. (2) Next we analyze the behaviour of noise assisted gradient descent on a ReLU gate in the realizable setting. While making no further distributional assumptions, we locate a ball centered at the origin such that all the iterates remain inside it with high probability. (3) Lastly we demonstrate a non-gradient iterative algorithm for which we give near optimal guarantees for training a class of depth-2 neural networks in the presence of an adversary who is additively corrupting the true labels. This analysis brings to light the advantage of having a large width for the network while defending against an adversary. We demonstrate that faced with data poisoning attacks of the kind we instantiate, for our chosen class of nets, the accuracy achieved by the algorithm in recovering the ground truth parameters, scales inversely with the width.

Guarantees on learning depth-2 neural networks under a data-poisoning attack

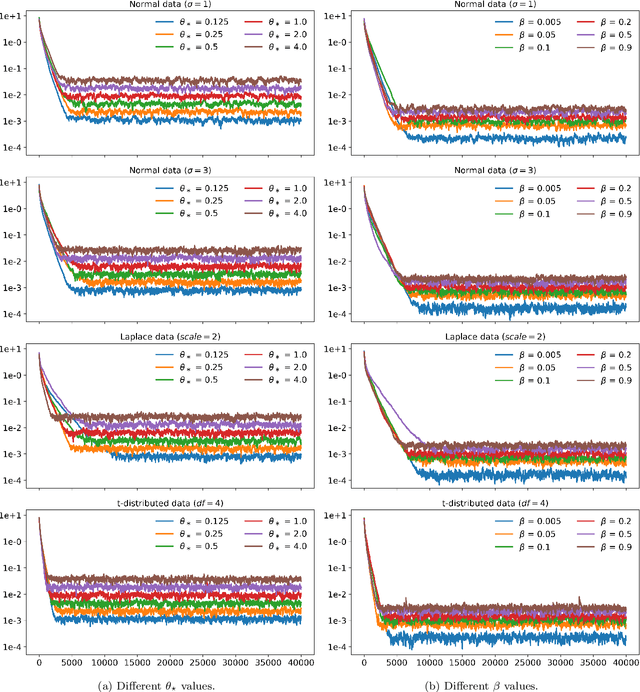
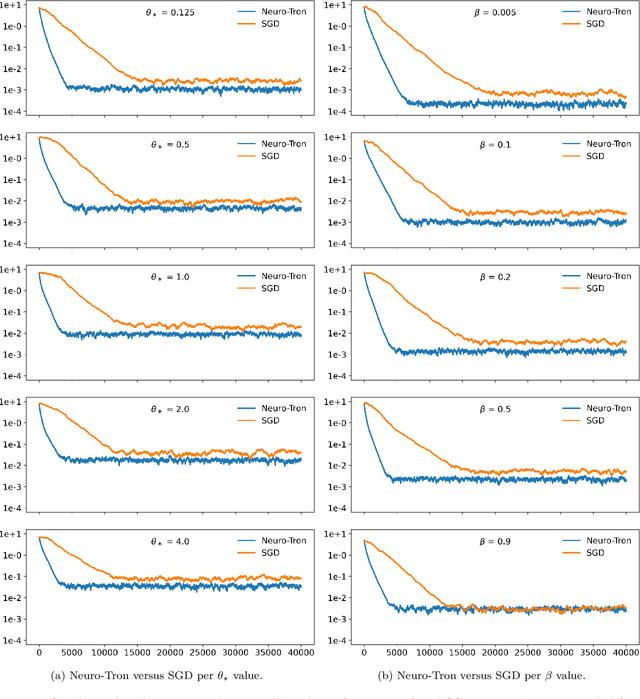
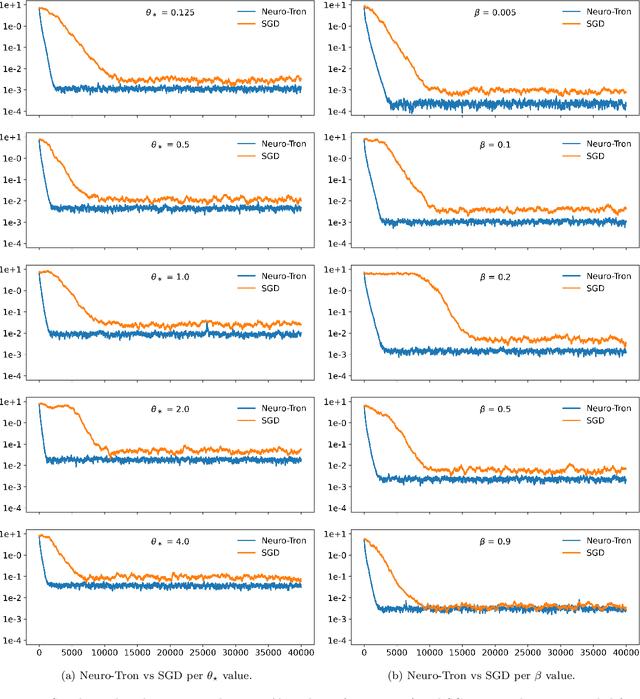
In recent times many state-of-the-art machine learning models have been shown to be fragile to adversarial attacks. In this work we attempt to build our theoretical understanding of adversarially robust learning with neural nets. We demonstrate a specific class of neural networks of finite size and a non-gradient stochastic algorithm which tries to recover the weights of the net generating the realizable true labels in the presence of an oracle doing a bounded amount of malicious additive distortion to the labels. We prove (nearly optimal) trade-offs among the magnitude of the adversarial attack, the accuracy and the confidence achieved by the proposed algorithm.