A Study of Neural Training with Non-Gradient and Noise Assisted Gradient Methods

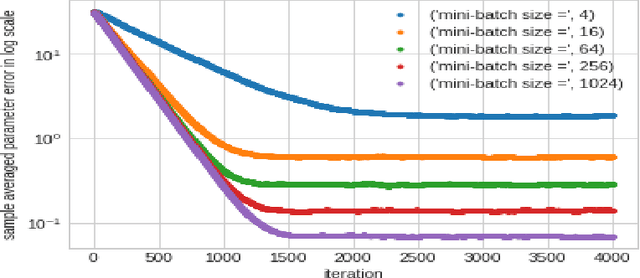
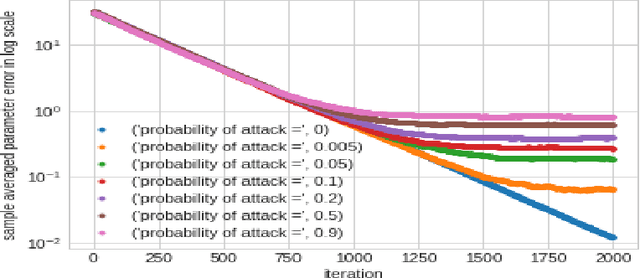
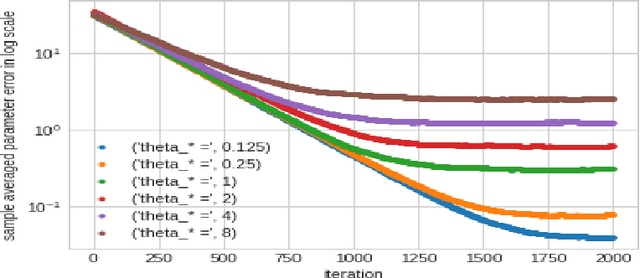
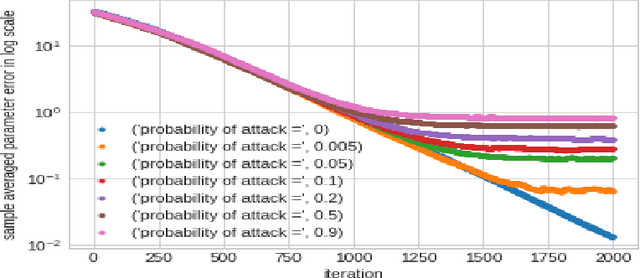
In this work we demonstrate provable guarantees on the training of depth-2 neural networks in new regimes than previously explored. (1) We start with a simple stochastic algorithm that can train a ReLU gate in the realizable setting with significantly milder conditions on the data distribution than previous results. Leveraging some additional distributional assumptions we also show near-optimal guarantees of training a ReLU gate when an adversary is allowed to corrupt the true labels. (2) Next we analyze the behaviour of noise assisted gradient descent on a ReLU gate in the realizable setting. While making no further distributional assumptions, we locate a ball centered at the origin such that all the iterates remain inside it with high probability. (3) Lastly we demonstrate a non-gradient iterative algorithm for which we give near optimal guarantees for training a class of depth-2 neural networks in the presence of an adversary who is additively corrupting the true labels. This analysis brings to light the advantage of having a large width for the network while defending against an adversary. We demonstrate that faced with data poisoning attacks of the kind we instantiate, for our chosen class of nets, the accuracy achieved by the algorithm in recovering the ground truth parameters, scales inversely with the width.