What is the cost of adding a constraint in linear least squares?

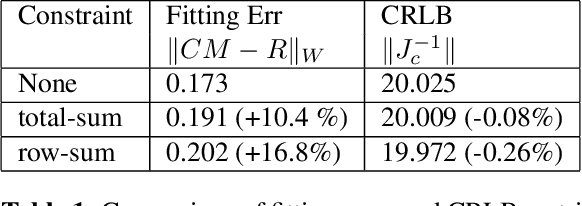
Although the theory of constrained least squares (CLS) estimation is well known, it is usually applied with the view that the constraints to be imposed are unavoidable. However, there are cases in which constraints are optional. For example, in camera color calibration, one of several possible color processing systems is obtained if a constraint on the row sums of a desired color correction matrix is imposed; in this example, it is not clear a priori whether imposing the constraint leads to better system performance. In this paper, we derive an exact expression connecting the constraint to the increase in fitting error obtained from imposing it. As another contribution, we show how to determine projection matrices that separate the measured data into two components: the first component drives up the fitting error due to imposing a constraint, and the second component is unaffected by the constraint. We demonstrate the use of these results in the color calibration problem.

Perceptually Motivated Shape Context Which Uses Shape Interiors

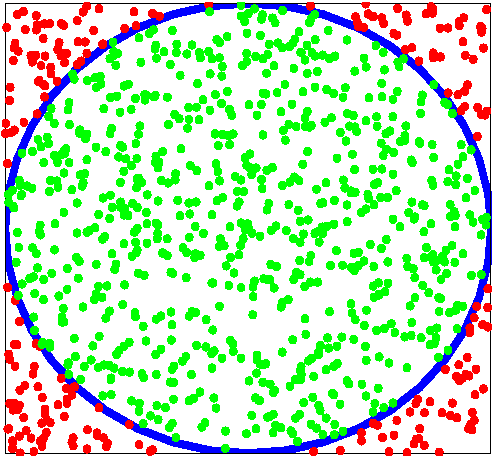
In this paper, we identify some of the limitations of current-day shape matching techniques. We provide examples of how contour-based shape matching techniques cannot provide a good match for certain visually similar shapes. To overcome this limitation, we propose a perceptually motivated variant of the well-known shape context descriptor. We identify that the interior properties of the shape play an important role in object recognition and develop a descriptor that captures these interior properties. We show that our method can easily be augmented with any other shape matching algorithm. We also show from our experiments that the use of our descriptor can significantly improve the retrieval rates.

A phase-sensitive method for filtering on the sphere

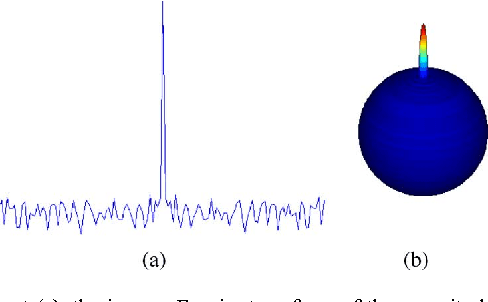
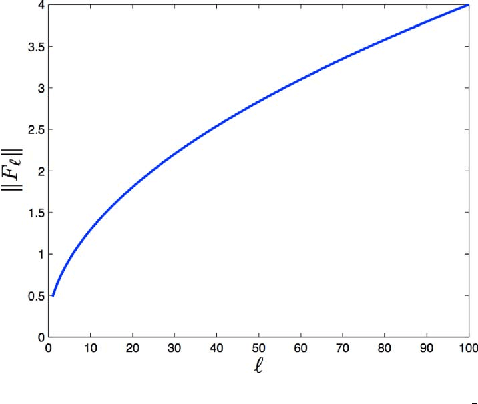
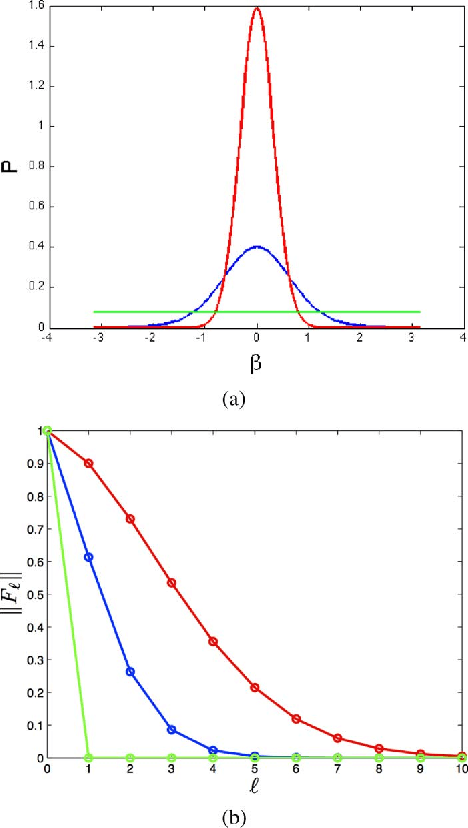
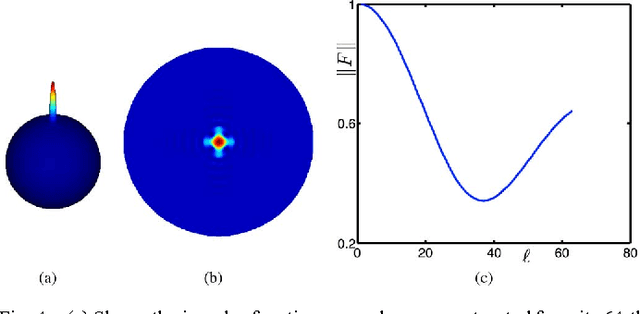
This paper examines filtering on a sphere, by first examining the roles of spherical harmonic magnitude and phase. We show that phase is more important than magnitude in determining the structure of a spherical function. We examine the properties of linear phase shifts in the spherical harmonic domain, which suggest a mechanism for constructing finite-impulse-response (FIR) filters. We show that those filters have desirable properties, such as being associative, mapping spherical functions to spherical functions, allowing directional filtering, and being defined by relatively simple equations. We provide examples of the filters for both spherical and manifold data.

Parametric annealing: a stochastic search method for human pose tracking

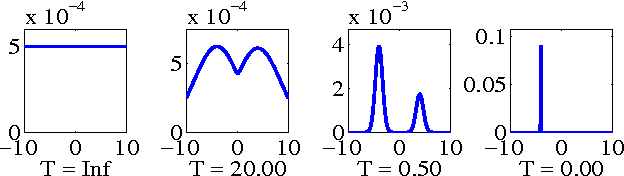
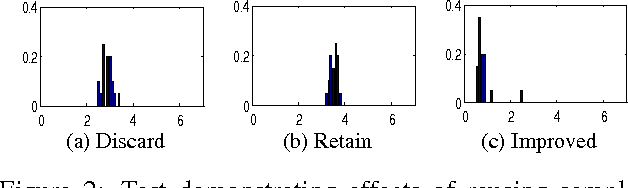
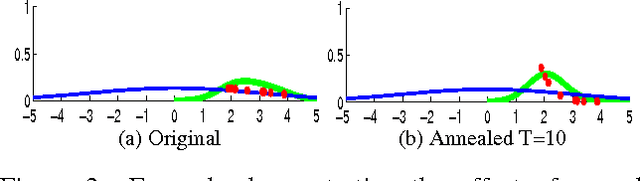
Model based methods to marker-free motion capture have a very high computational overhead that make them unattractive. In this paper we describe a method that improves on existing global optimization techniques to tracking articulated objects. Our method improves on the state-of-the-art Annealed Particle Filter (APF) by reusing samples across annealing layers and by using an adaptive parametric density for diffusion. We compare the proposed method with APF on a scalable problem and study how the two methods scale with the dimensionality, multi-modality and the range of search. Then we perform sensitivity analysis on the parameters of our algorithm and show that it tolerates a wide range of parameter settings. We also show results on tracking human pose from the widely-used Human Eva I dataset. Our results show that the proposed method reduces the tracking error despite using less than 50% of the computational resources as APF. The tracked output also shows a significant qualitative improvement over APF as demonstrated through image and video results.