A phase-sensitive method for filtering on the sphere
Paper and Code
Aug 03, 2012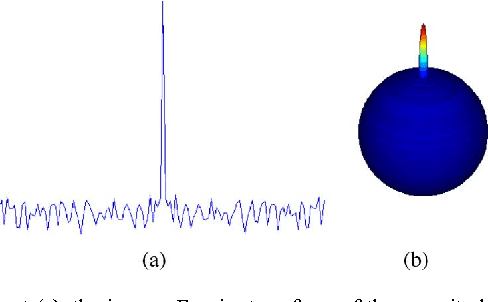
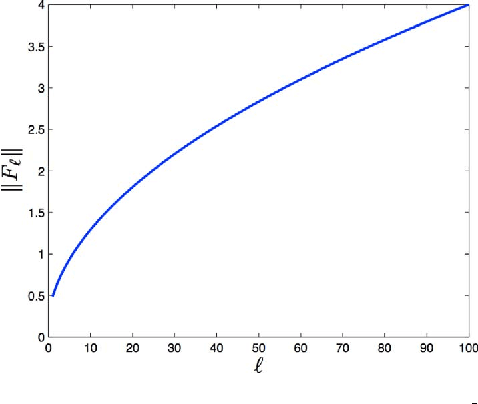
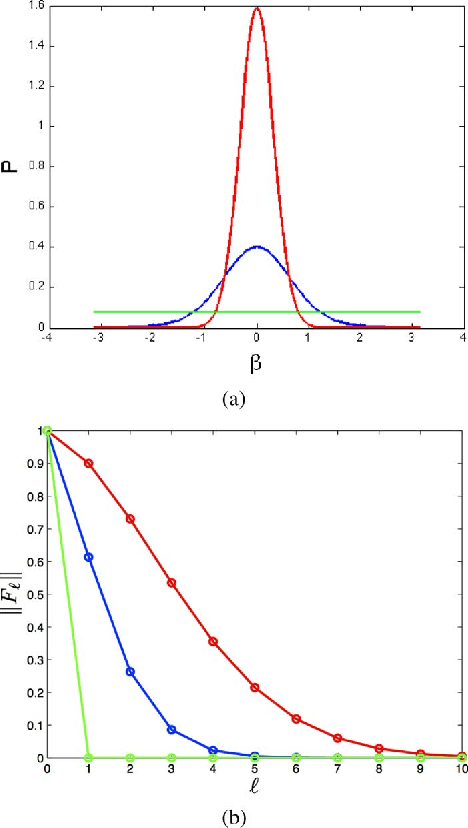
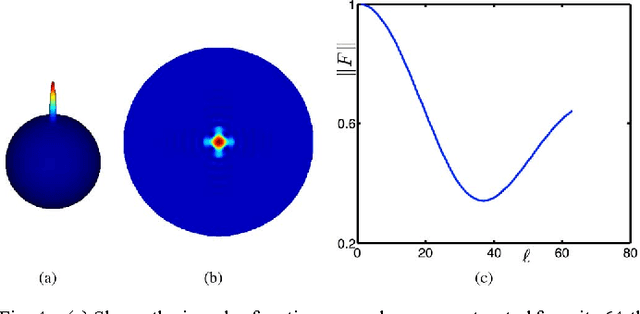
This paper examines filtering on a sphere, by first examining the roles of spherical harmonic magnitude and phase. We show that phase is more important than magnitude in determining the structure of a spherical function. We examine the properties of linear phase shifts in the spherical harmonic domain, which suggest a mechanism for constructing finite-impulse-response (FIR) filters. We show that those filters have desirable properties, such as being associative, mapping spherical functions to spherical functions, allowing directional filtering, and being defined by relatively simple equations. We provide examples of the filters for both spherical and manifold data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge