Clinical trial site matching with improved diversity using fair policy learning

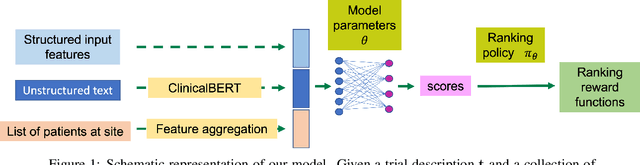
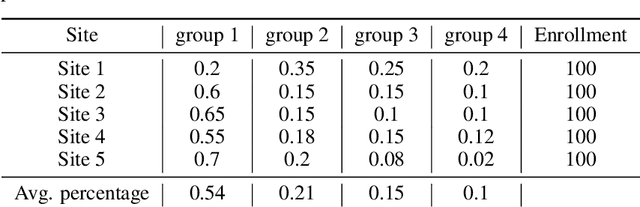
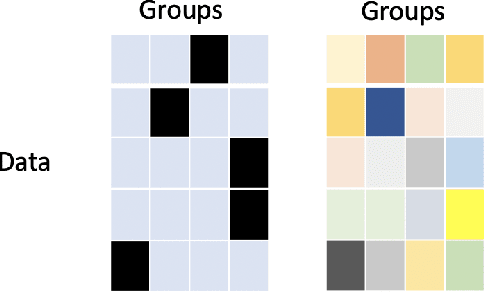
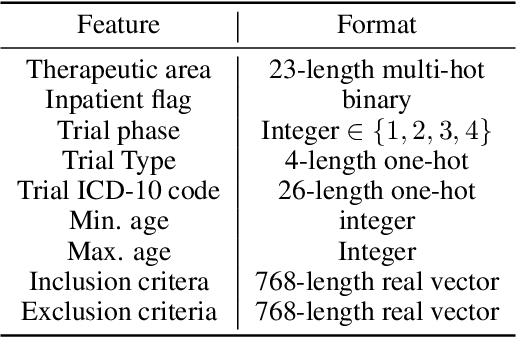
The ongoing pandemic has highlighted the importance of reliable and efficient clinical trials in healthcare. Trial sites, where the trials are conducted, are chosen mainly based on feasibility in terms of medical expertise and access to a large group of patients. More recently, the issue of diversity and inclusion in clinical trials is gaining importance. Different patient groups may experience the effects of a medical drug/ treatment differently and hence need to be included in the clinical trials. These groups could be based on ethnicity, co-morbidities, age, or economic factors. Thus, designing a method for trial site selection that accounts for both feasibility and diversity is a crucial and urgent goal. In this paper, we formulate this problem as a ranking problem with fairness constraints. Using principles of fairness in machine learning, we learn a model that maps a clinical trial description to a ranked list of potential trial sites. Unlike existing fairness frameworks, the group membership of each trial site is non-binary: each trial site may have access to patients from multiple groups. We propose fairness criteria based on demographic parity to address such a multi-group membership scenario. We test our method on 480 real-world clinical trials and show that our model results in a list of potential trial sites that provides access to a diverse set of patients while also ensuing a high number of enrolled patients.

Fast Graph Attention Networks Using Effective Resistance Based Graph Sparsification

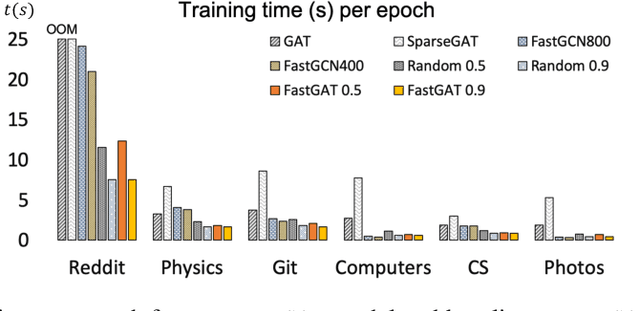
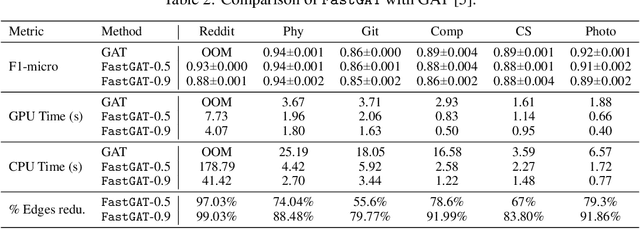
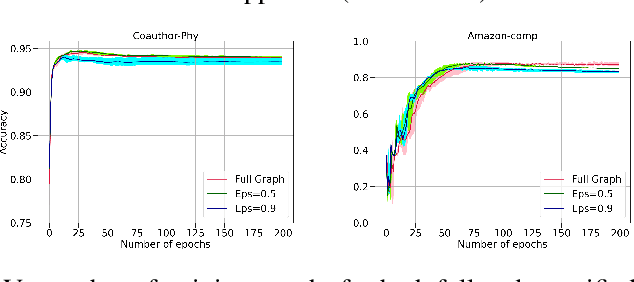
The attention mechanism has demonstrated superior performance for inference over nodes in graph neural networks (GNNs), however, they result in a high computational burden during both training and inference. We propose FastGAT, a method to make attention based GNNs lightweight by using spectral sparsification to generate an optimal pruning of the input graph. This results in a per-epoch time that is almost linear in the number of graph nodes as opposed to quadratic. Further, we provide a re-formulation of a specific attention based GNN, Graph Attention Network (GAT) that interprets it as a graph convolution method using the random walk normalized graph Laplacian. Using this framework, we theoretically prove that spectral sparsification preserves the features computed by the GAT model, thereby justifying our FastGAT algorithm. We experimentally evaluate FastGAT on several large real world graph datasets for node classification tasks, FastGAT can dramatically reduce (up to 10x) the computational time and memory requirements, allowing the usage of attention based GNNs on large graphs.

Localized sketching for matrix multiplication and ridge regression

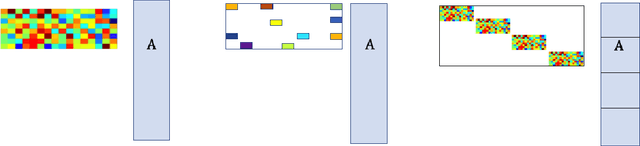
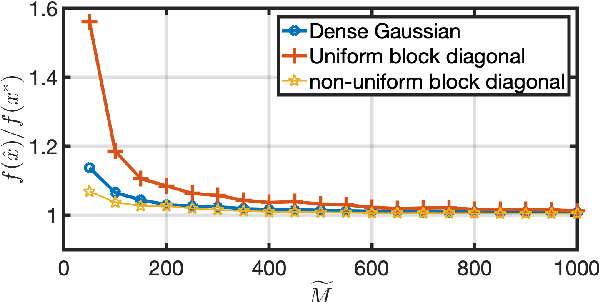
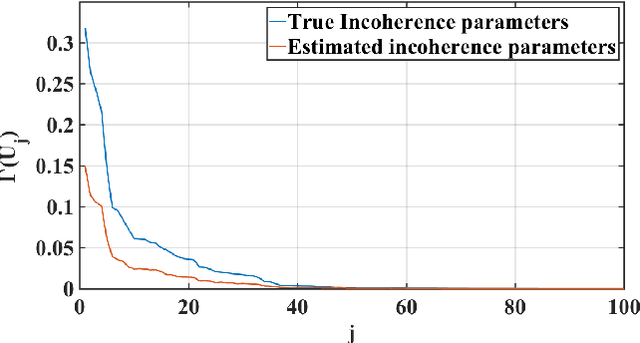
We consider sketched approximate matrix multiplication and ridge regression in the novel setting of localized sketching, where at any given point, only part of the data matrix is available. This corresponds to a block diagonal structure on the sketching matrix. We show that, under mild conditions, block diagonal sketching matrices require only O(stable rank / \epsilon^2) and $O( stat. dim. \epsilon)$ total sample complexity for matrix multiplication and ridge regression, respectively. This matches the state-of-the-art bounds that are obtained using global sketching matrices. The localized nature of sketching considered allows for different parts of the data matrix to be sketched independently and hence is more amenable to computation in distributed and streaming settings and results in a smaller memory and computational footprint.