InVA: Integrative Variational Autoencoder for Harmonization of Multi-modal Neuroimaging Data

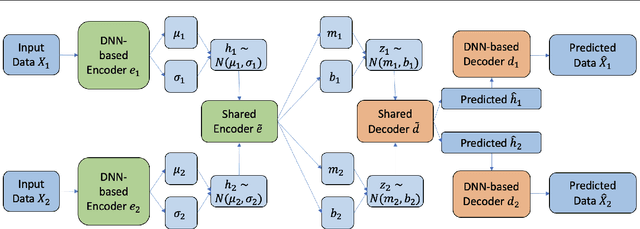
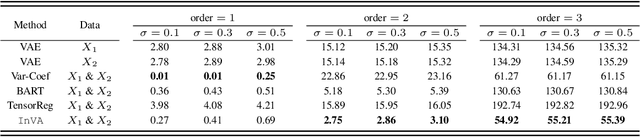
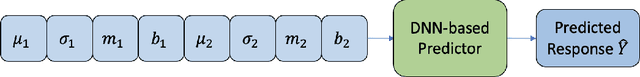
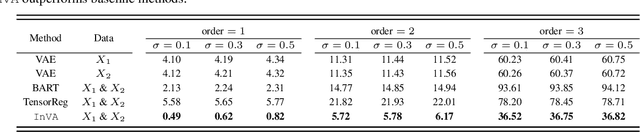
There is a significant interest in exploring non-linear associations among multiple images derived from diverse imaging modalities. While there is a growing literature on image-on-image regression to delineate predictive inference of an image based on multiple images, existing approaches have limitations in efficiently borrowing information between multiple imaging modalities in the prediction of an image. Building on the literature of Variational Auto Encoders (VAEs), this article proposes a novel approach, referred to as Integrative Variational Autoencoder (\texttt{InVA}) method, which borrows information from multiple images obtained from different sources to draw predictive inference of an image. The proposed approach captures complex non-linear association between the outcome image and input images, while allowing rapid computation. Numerical results demonstrate substantial advantages of \texttt{InVA} over VAEs, which typically do not allow borrowing information between input images. The proposed framework offers highly accurate predictive inferences for costly positron emission topography (PET) from multiple measures of cortical structure in human brain scans readily available from magnetic resonance imaging (MRI).

Bayesian Conditional Density Filtering

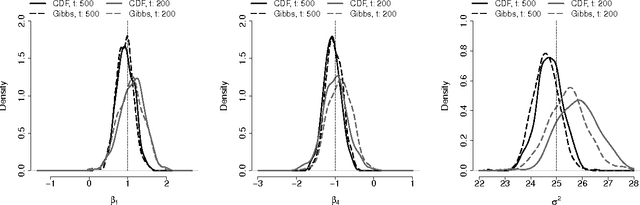
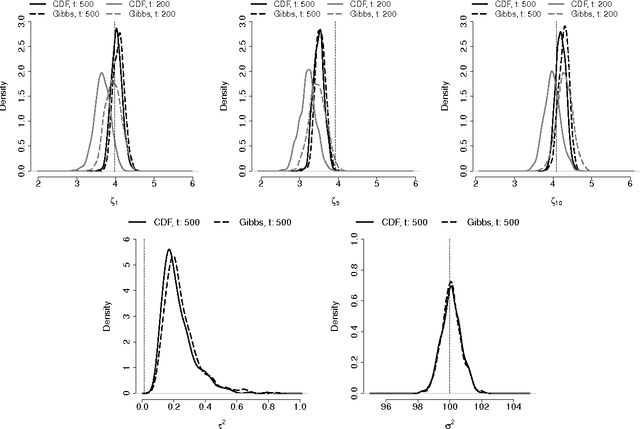
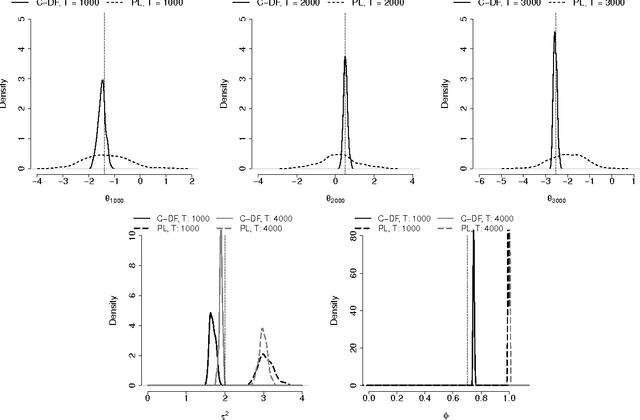
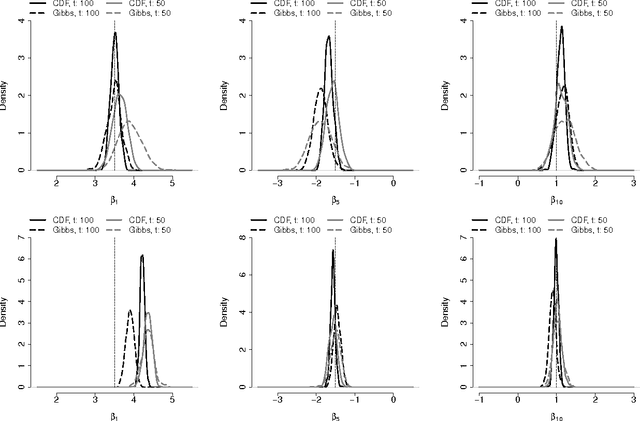
We propose a Conditional Density Filtering (C-DF) algorithm for efficient online Bayesian inference. C-DF adapts MCMC sampling to the online setting, sampling from approximations to conditional posterior distributions obtained by propagating surrogate conditional sufficient statistics (a function of data and parameter estimates) as new data arrive. These quantities eliminate the need to store or process the entire dataset simultaneously and offer a number of desirable features. Often, these include a reduction in memory requirements and runtime and improved mixing, along with state-of-the-art parameter inference and prediction. These improvements are demonstrated through several illustrative examples including an application to high dimensional compressed regression. Finally, we show that C-DF samples converge to the target posterior distribution asymptotically as sampling proceeds and more data arrives.

Compressed Gaussian Process

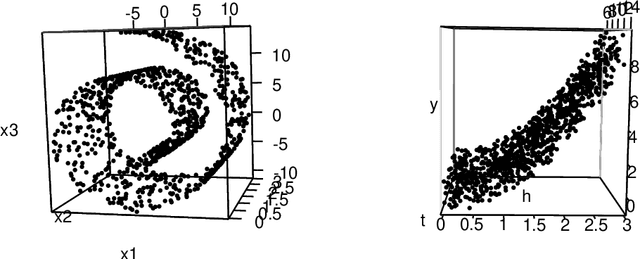
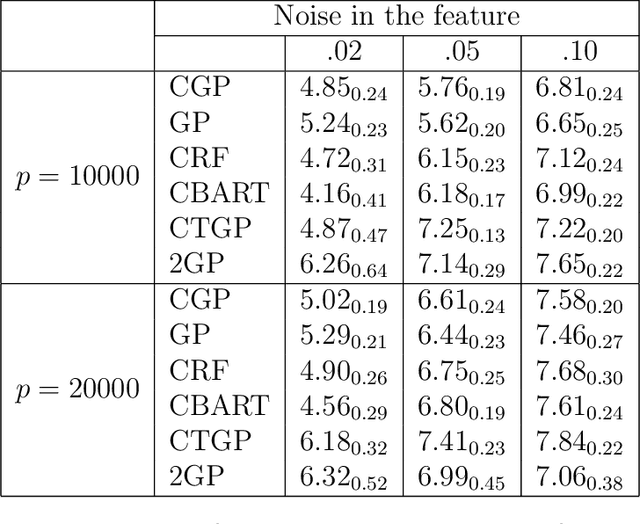
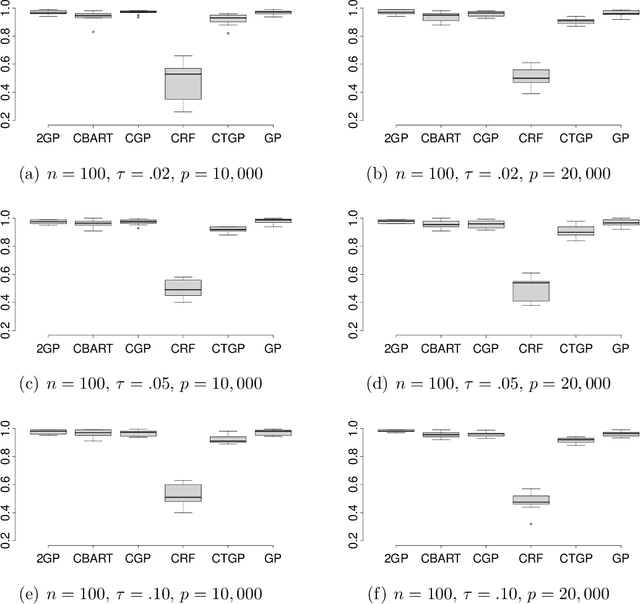
Nonparametric regression for massive numbers of samples (n) and features (p) is an increasingly important problem. In big n settings, a common strategy is to partition the feature space, and then separately apply simple models to each partition set. We propose an alternative approach, which avoids such partitioning and the associated sensitivity to neighborhood choice and distance metrics, by using random compression combined with Gaussian process regression. The proposed approach is particularly motivated by the setting in which the response is conditionally independent of the features given the projection to a low dimensional manifold. Conditionally on the random compression matrix and a smoothness parameter, the posterior distribution for the regression surface and posterior predictive distributions are available analytically. Running the analysis in parallel for many random compression matrices and smoothness parameters, model averaging is used to combine the results. The algorithm can be implemented rapidly even in very big n and p problems, has strong theoretical justification, and is found to yield state of the art predictive performance.

Bayesian Compressed Regression

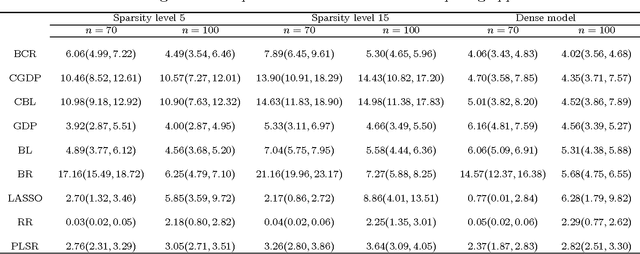
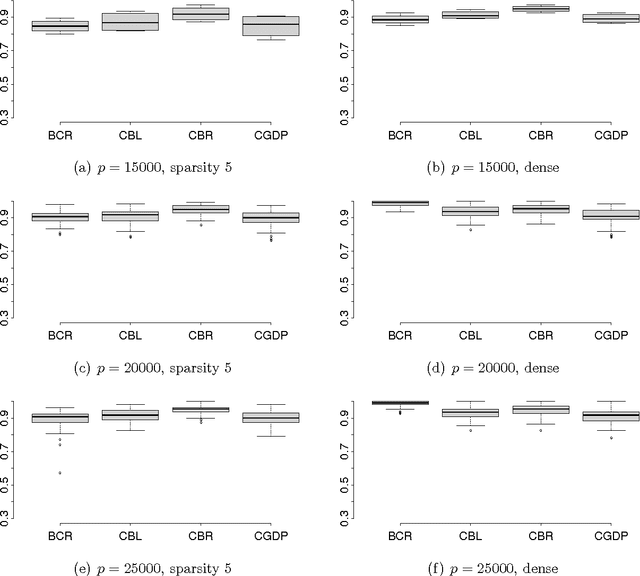
As an alternative to variable selection or shrinkage in high dimensional regression, we propose to randomly compress the predictors prior to analysis. This dramatically reduces storage and computational bottlenecks, performing well when the predictors can be projected to a low dimensional linear subspace with minimal loss of information about the response. As opposed to existing Bayesian dimensionality reduction approaches, the exact posterior distribution conditional on the compressed data is available analytically, speeding up computation by many orders of magnitude while also bypassing robustness issues due to convergence and mixing problems with MCMC. Model averaging is used to reduce sensitivity to the random projection matrix, while accommodating uncertainty in the subspace dimension. Strong theoretical support is provided for the approach by showing near parametric convergence rates for the predictive density in the large p small n asymptotic paradigm. Practical performance relative to competitors is illustrated in simulations and real data applications.