Compressed Gaussian Process
Paper and Code
Jun 07, 2014
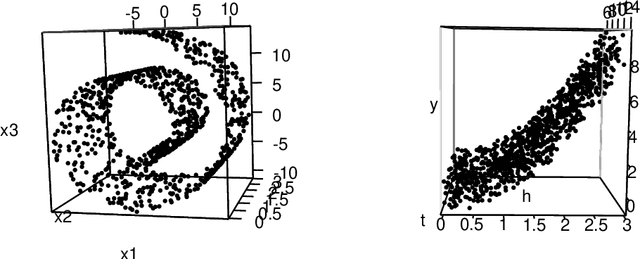
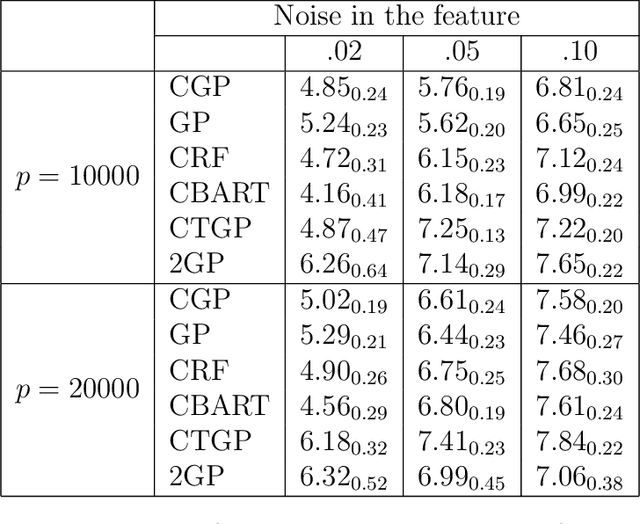
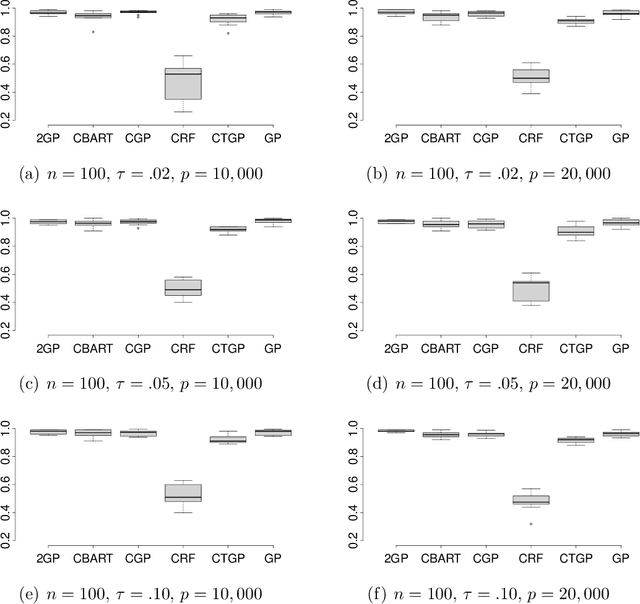
Nonparametric regression for massive numbers of samples (n) and features (p) is an increasingly important problem. In big n settings, a common strategy is to partition the feature space, and then separately apply simple models to each partition set. We propose an alternative approach, which avoids such partitioning and the associated sensitivity to neighborhood choice and distance metrics, by using random compression combined with Gaussian process regression. The proposed approach is particularly motivated by the setting in which the response is conditionally independent of the features given the projection to a low dimensional manifold. Conditionally on the random compression matrix and a smoothness parameter, the posterior distribution for the regression surface and posterior predictive distributions are available analytically. Running the analysis in parallel for many random compression matrices and smoothness parameters, model averaging is used to combine the results. The algorithm can be implemented rapidly even in very big n and p problems, has strong theoretical justification, and is found to yield state of the art predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge