Shaan Qamar
Bayesian Conditional Density Filtering
Sep 22, 2015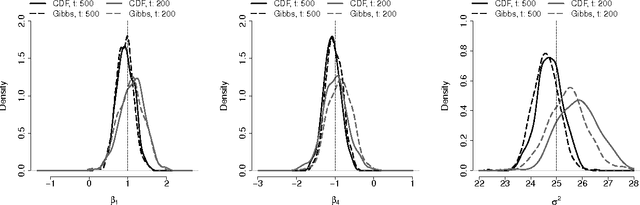
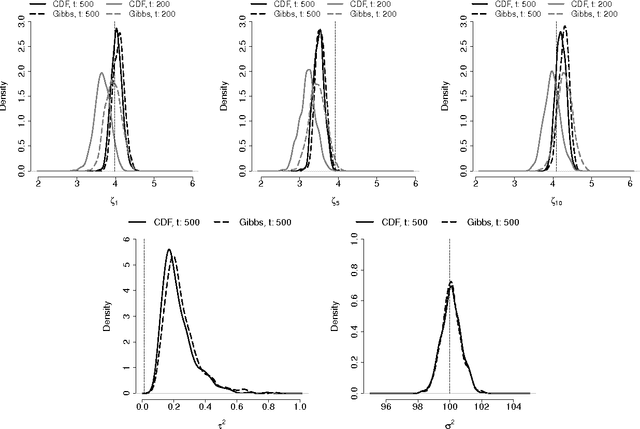
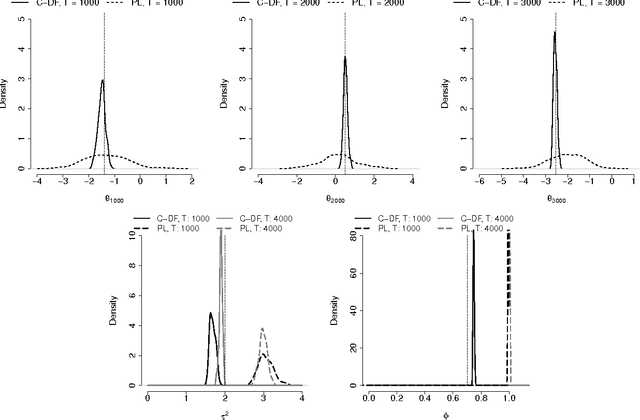
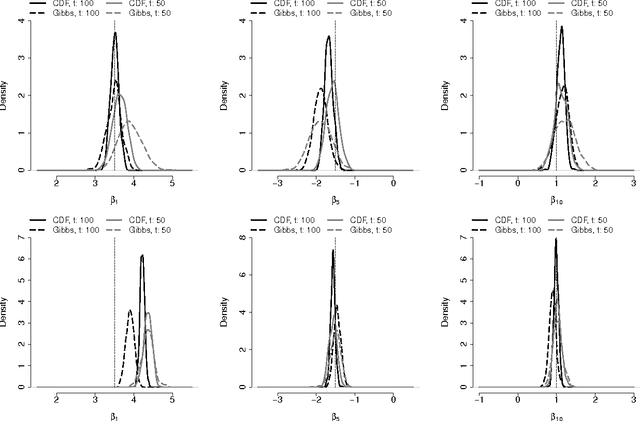
Abstract:We propose a Conditional Density Filtering (C-DF) algorithm for efficient online Bayesian inference. C-DF adapts MCMC sampling to the online setting, sampling from approximations to conditional posterior distributions obtained by propagating surrogate conditional sufficient statistics (a function of data and parameter estimates) as new data arrive. These quantities eliminate the need to store or process the entire dataset simultaneously and offer a number of desirable features. Often, these include a reduction in memory requirements and runtime and improved mixing, along with state-of-the-art parameter inference and prediction. These improvements are demonstrated through several illustrative examples including an application to high dimensional compressed regression. Finally, we show that C-DF samples converge to the target posterior distribution asymptotically as sampling proceeds and more data arrives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge