Intrinsic Sliced Wasserstein Distances for Comparing Collections of Probability Distributions on Manifolds and Graphs

Collections of probability distributions arise in a variety of statistical applications ranging from user activity pattern analysis to brain connectomics. In practice these distributions are represented by histograms over diverse domain types including finite intervals, circles, cylinders, spheres, other manifolds, and graphs. This paper introduces an approach for detecting differences between two collections of histograms over such general domains. To this end, we introduce the intrinsic slicing construction that yields a novel class of Wasserstein distances on manifolds and graphs. These distances are Hilbert embeddable, which allows us to reduce the histogram collection comparison problem to the comparison of means in a high-dimensional Euclidean space. We develop a hypothesis testing procedure based on conducting t-tests on each dimension of this embedding, then combining the resulting p-values using recently proposed p-value combination techniques. Our numerical experiments in a variety of data settings show that the resulting tests are powerful and the p-values are well-calibrated. Example applications to user activity patterns, spatial data, and brain connectomics are provided.

Kernel Mean Embedding Based Hypothesis Tests for Comparing Spatial Point Patterns

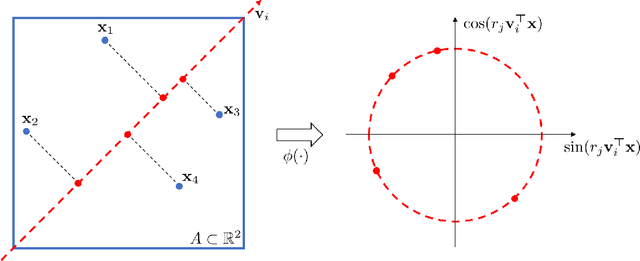
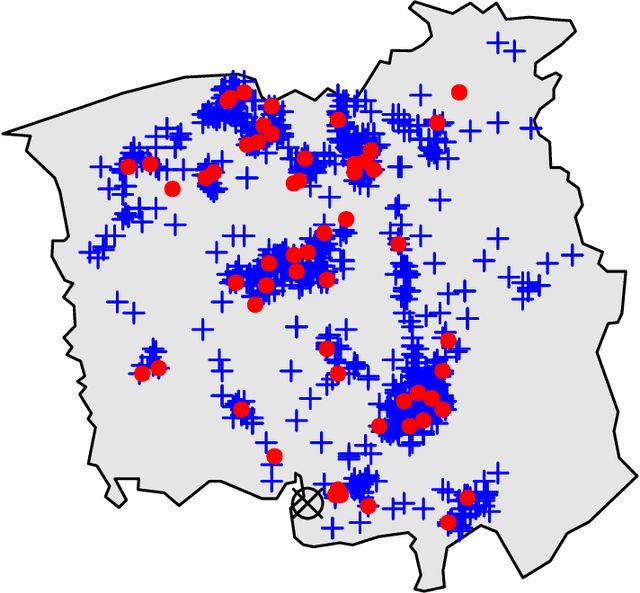
This paper introduces an approach for detecting differences in the first-order structures of spatial point patterns. The proposed approach leverages the kernel mean embedding in a novel way by introducing its approximate version tailored to spatial point processes. While the original embedding is infinite-dimensional and implicit, our approximate embedding is finite-dimensional and comes with explicit closed-form formulas. With its help we reduce the pattern comparison problem to the comparison of means in the Euclidean space. Hypothesis testing is based on conducting $t$-tests on each dimension of the embedding and combining the resulting $p$-values using the harmonic mean $p$-value combination technique. The main advantages of the proposed approach are that it can be applied to both single and replicated pattern comparisons, and that neither bootstrap nor permutation procedures are needed to obtain or calibrate the $p$-values. Our experiments show that the resulting tests are powerful and the $p$-values are well-calibrated; two applications to real world data are presented.

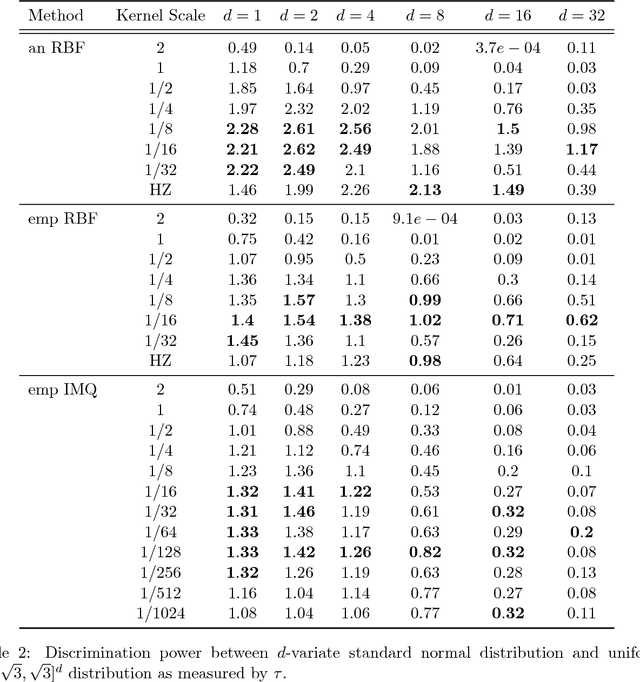
Closed-form Expressions for Maximum Mean Discrepancy with Applications to Wasserstein Auto-Encoders

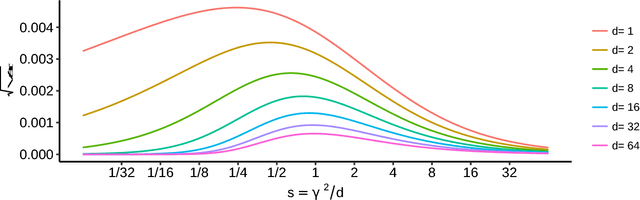
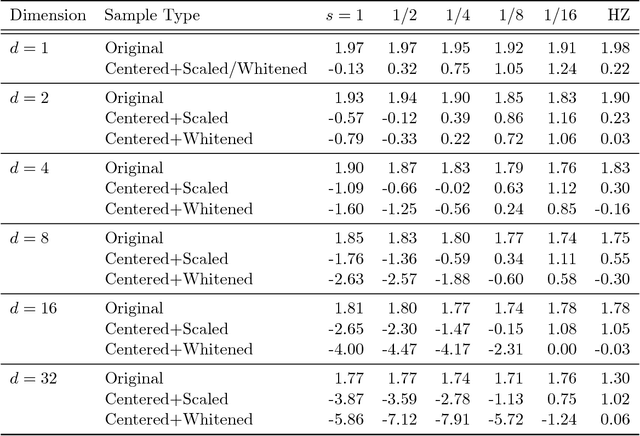
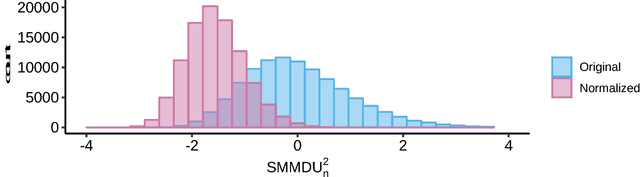
The Maximum Mean Discrepancy (MMD) has found numerous applications in statistics and machine learning, most recently as a penalty in the Wasserstein Auto-Encoder (WAE). In this paper we compute closed-form expressions for estimating the Gaussian kernel based MMD between a given distribution and the standard multivariate normal distribution. We introduce the standardized version of MMD as a penalty for the WAE training objective, allowing for a better interpretability of MMD values and more compatibility across different hyperparameter settings. Next, we propose using a version of batch normalization at the code layer; this has the benefits of making the kernel width selection easier, reducing the training effort, and preventing outliers in the aggregate code distribution. Finally, we discuss the appropriate null distributions and provide thresholds for multivariate normality testing with the standardized MMD, leading to a number of easy rules of thumb for monitoring the progress of WAE training. Curiously, our MMD formula reveals a connection to the Baringhaus-Henze-Epps-Pulley (BHEP) statistic of the Henze-Zirkler test and provides further insights about the MMD. Our experiments on synthetic and real data show that the analytic formulation improves over the commonly used stochastic approximation of the MMD, and demonstrate that code normalization provides significant benefits when training WAEs.

Graph Matching with Anchor Nodes: A Learning Approach

In this paper, we consider the weighted graph matching problem with partially disclosed correspondences between a number of anchor nodes. Our construction exploits recently introduced node signatures based on graph Laplacians, namely the Laplacian family signature (LFS) on the nodes, and the pairwise heat kernel map on the edges. In this paper, without assuming an explicit form of parametric dependence nor a distance metric between node signatures, we formulate an optimization problem which incorporates the knowledge of anchor nodes. Solving this problem gives us an optimized proximity measure specific to the graphs under consideration. Using this as a first order compatibility term, we then set up an integer quadratic program (IQP) to solve for a near optimal graph matching. Our experiments demonstrate the superior performance of our approach on randomly generated graphs and on two widely-used image sequences, when compared with other existing signature and adjacency matrix based graph matching methods.

Stable and Informative Spectral Signatures for Graph Matching

In this paper, we consider the approximate weighted graph matching problem and introduce stable and informative first and second order compatibility terms suitable for inclusion into the popular integer quadratic program formulation. Our approach relies on a rigorous analysis of stability of spectral signatures based on the graph Laplacian. In the case of the first order term, we derive an objective function that measures both the stability and informativeness of a given spectral signature. By optimizing this objective, we design new spectral node signatures tuned to a specific graph to be matched. We also introduce the pairwise heat kernel distance as a stable second order compatibility term; we justify its plausibility by showing that in a certain limiting case it converges to the classical adjacency matrix-based second order compatibility function. We have tested our approach on a set of synthetic graphs, the widely-used CMU house sequence, and a set of real images. These experiments show the superior performance of our first and second order compatibility terms as compared with the commonly used ones.

Interpretable Graph-Based Semi-Supervised Learning via Flows

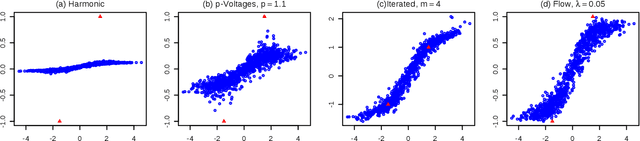
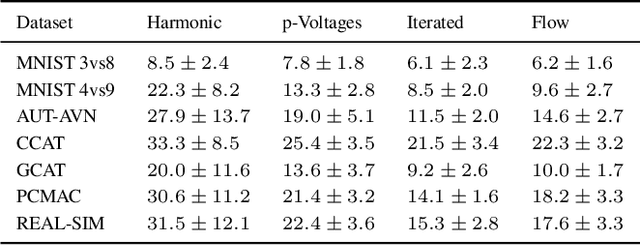
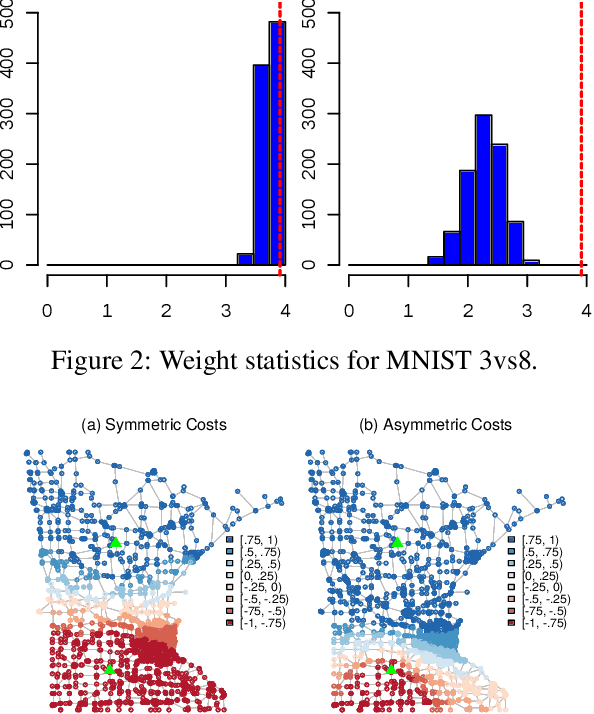
In this paper, we consider the interpretability of the foundational Laplacian-based semi-supervised learning approaches on graphs. We introduce a novel flow-based learning framework that subsumes the foundational approaches and additionally provides a detailed, transparent, and easily understood expression of the learning process in terms of graph flows. As a result, one can visualize and interactively explore the precise subgraph along which the information from labeled nodes flows to an unlabeled node of interest. Surprisingly, the proposed framework avoids trading accuracy for interpretability, but in fact leads to improved prediction accuracy, which is supported both by theoretical considerations and empirical results. The flow-based framework guarantees the maximum principle by construction and can handle directed graphs in an out-of-the-box manner.

Average Interpolating Wavelets on Point Clouds and Graphs

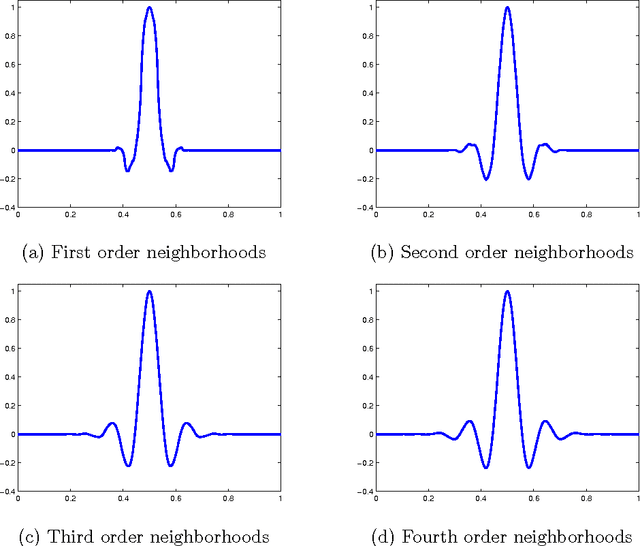
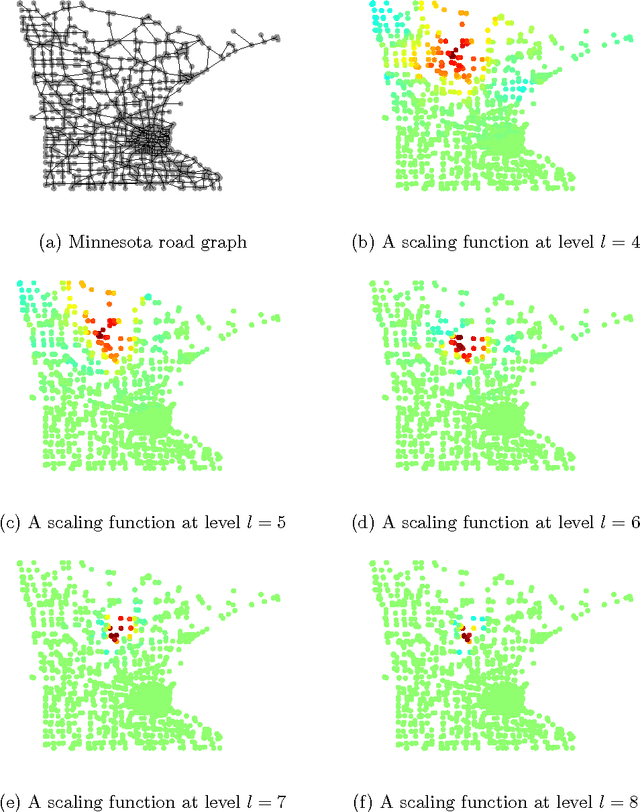
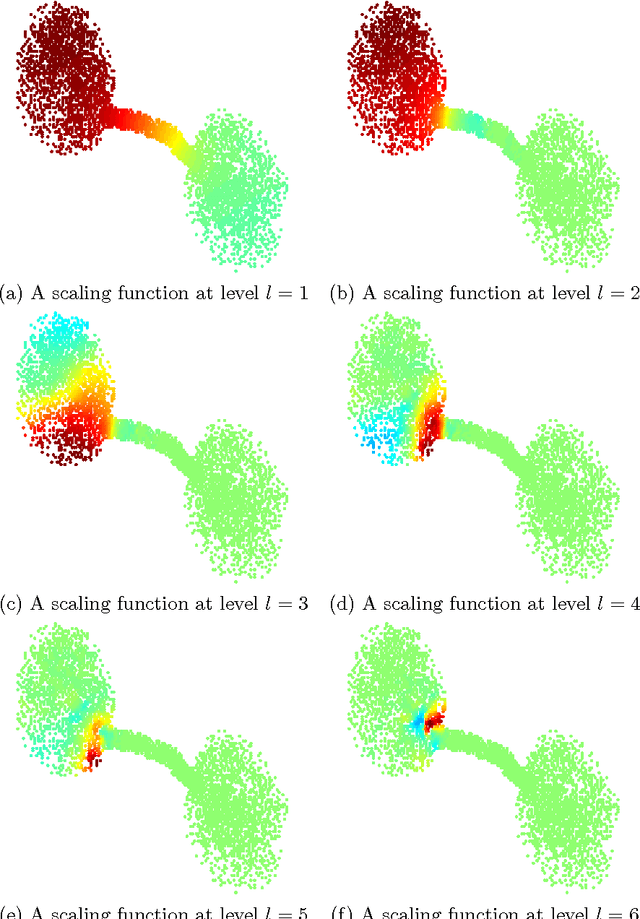
We introduce a new wavelet transform suitable for analyzing functions on point clouds and graphs. Our construction is based on a generalization of the average interpolating refinement scheme of Donoho. The most important ingredient of the original scheme that needs to be altered is the choice of the interpolant. Here, we define the interpolant as the minimizer of a smoothness functional, namely a generalization of the Laplacian energy, subject to the averaging constraints. In the continuous setting, we derive a formula for the optimal solution in terms of the poly-harmonic Green's function. The form of this solution is used to motivate our construction in the setting of graphs and point clouds. We highlight the empirical convergence of our refinement scheme and the potential applications of the resulting wavelet transform through experiments on a number of data stets.