Kernel Mean Embedding Based Hypothesis Tests for Comparing Spatial Point Patterns
Paper and Code
May 31, 2019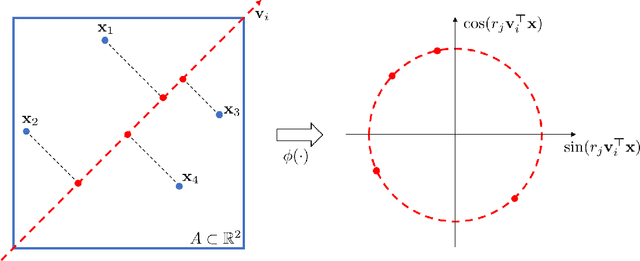


This paper introduces an approach for detecting differences in the first-order structures of spatial point patterns. The proposed approach leverages the kernel mean embedding in a novel way by introducing its approximate version tailored to spatial point processes. While the original embedding is infinite-dimensional and implicit, our approximate embedding is finite-dimensional and comes with explicit closed-form formulas. With its help we reduce the pattern comparison problem to the comparison of means in the Euclidean space. Hypothesis testing is based on conducting $t$-tests on each dimension of the embedding and combining the resulting $p$-values using the harmonic mean $p$-value combination technique. The main advantages of the proposed approach are that it can be applied to both single and replicated pattern comparisons, and that neither bootstrap nor permutation procedures are needed to obtain or calibrate the $p$-values. Our experiments show that the resulting tests are powerful and the $p$-values are well-calibrated; two applications to real world data are presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge