Closed-form Expressions for Maximum Mean Discrepancy with Applications to Wasserstein Auto-Encoders

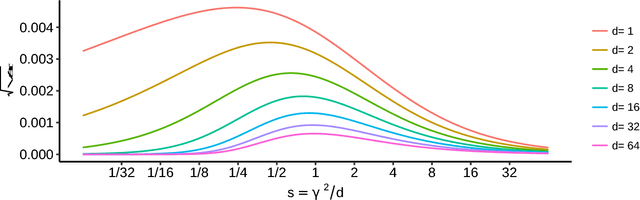
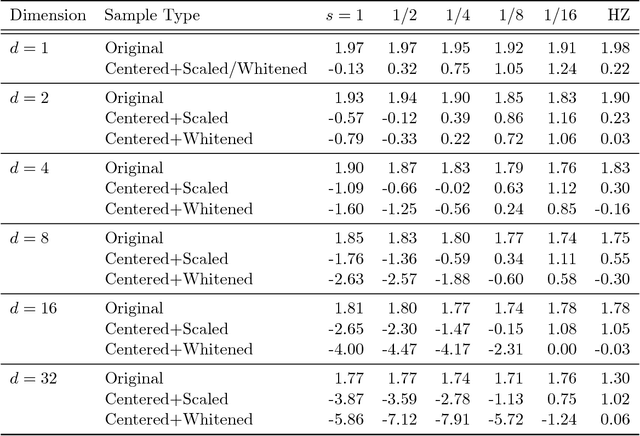
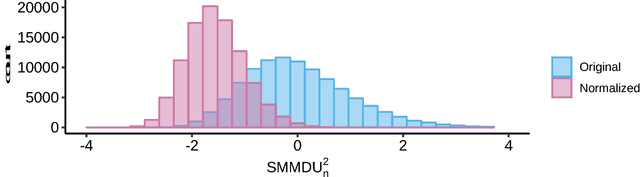
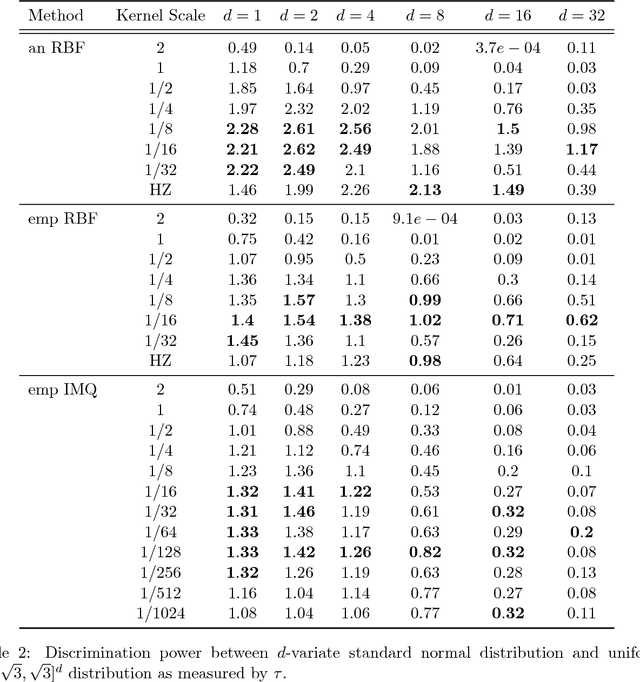
The Maximum Mean Discrepancy (MMD) has found numerous applications in statistics and machine learning, most recently as a penalty in the Wasserstein Auto-Encoder (WAE). In this paper we compute closed-form expressions for estimating the Gaussian kernel based MMD between a given distribution and the standard multivariate normal distribution. We introduce the standardized version of MMD as a penalty for the WAE training objective, allowing for a better interpretability of MMD values and more compatibility across different hyperparameter settings. Next, we propose using a version of batch normalization at the code layer; this has the benefits of making the kernel width selection easier, reducing the training effort, and preventing outliers in the aggregate code distribution. Finally, we discuss the appropriate null distributions and provide thresholds for multivariate normality testing with the standardized MMD, leading to a number of easy rules of thumb for monitoring the progress of WAE training. Curiously, our MMD formula reveals a connection to the Baringhaus-Henze-Epps-Pulley (BHEP) statistic of the Henze-Zirkler test and provides further insights about the MMD. Our experiments on synthetic and real data show that the analytic formulation improves over the commonly used stochastic approximation of the MMD, and demonstrate that code normalization provides significant benefits when training WAEs.