A Learning Framework for Self-Tuning Histograms

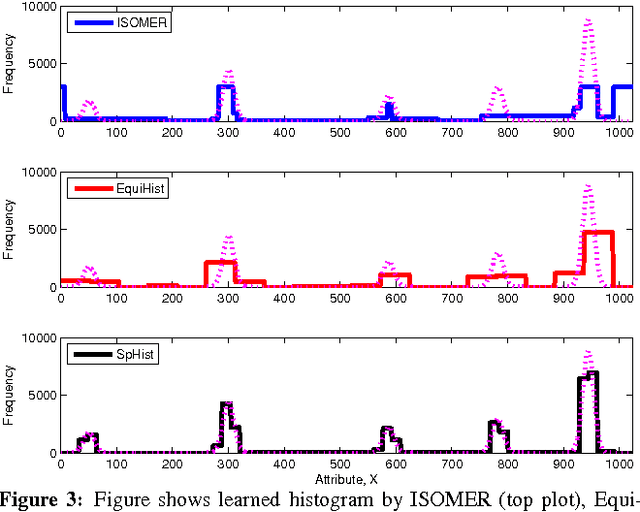
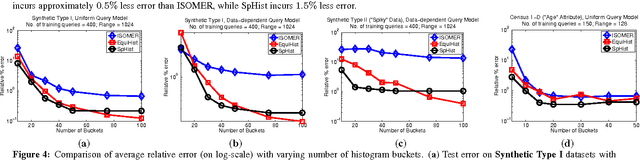
In this paper, we consider the problem of estimating self-tuning histograms using query workloads. To this end, we propose a general learning theoretic formulation. Specifically, we use query feedback from a workload as training data to estimate a histogram with a small memory footprint that minimizes the expected error on future queries. Our formulation provides a framework in which different approaches can be studied and developed. We first study the simple class of equi-width histograms and present a learning algorithm, EquiHist, that is competitive in many settings. We also provide formal guarantees for equi-width histograms that highlight scenarios in which equi-width histograms can be expected to succeed or fail. We then go beyond equi-width histograms and present a novel learning algorithm, SpHist, for estimating general histograms. Here we use Haar wavelets to reduce the problem of learning histograms to that of learning a sparse vector. Both algorithms have multiple advantages over existing methods: 1) simple and scalable extensions to multi-dimensional data, 2) scalability with number of histogram buckets and size of query feedback, 3) natural extensions to incorporate new feedback and handle database updates. We demonstrate these advantages over the current state-of-the-art, ISOMER, through detailed experiments on real and synthetic data. In particular, we show that SpHist obtains up to 50% less error than ISOMER on real-world multi-dimensional datasets.

Efficient Discovery of Large Synchronous Events in Neural Spike Streams

We address the problem of finding patterns from multi-neuronal spike trains that give us insights into the multi-neuronal codes used in the brain and help us design better brain computer interfaces. We focus on the synchronous firings of groups of neurons as these have been shown to play a major role in coding and communication. With large electrode arrays, it is now possible to simultaneously record the spiking activity of hundreds of neurons over large periods of time. Recently, techniques have been developed to efficiently count the frequency of synchronous firing patterns. However, when the number of neurons being observed grows they suffer from the combinatorial explosion in the number of possible patterns and do not scale well. In this paper, we present a temporal data mining scheme that overcomes many of these problems. It generates a set of candidate patterns from frequent patterns of smaller size; all possible patterns are not counted. Also we count only a certain well defined subset of occurrences and this makes the process more efficient. We highlight the computational advantage that this approach offers over the existing methods through simulations. We also propose methods for assessing the statistical significance of the discovered patterns. We detect only those patterns that repeat often enough to be significant and thus be able to automatically fix the threshold for the data-mining application. Finally we discuss the usefulness of these methods for brain computer interfaces.

Discovering general partial orders in event streams

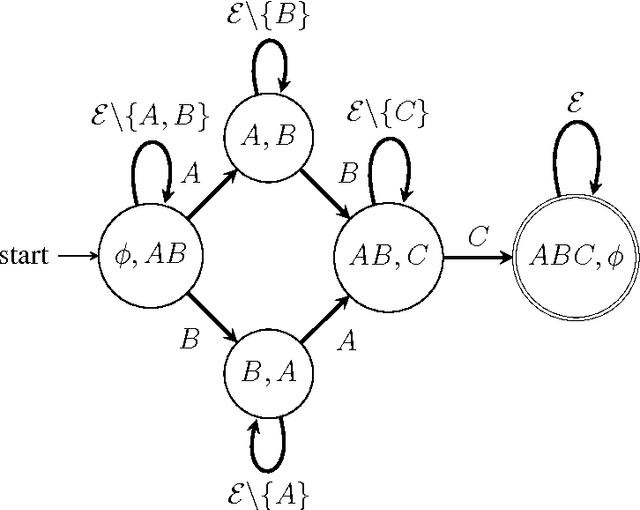
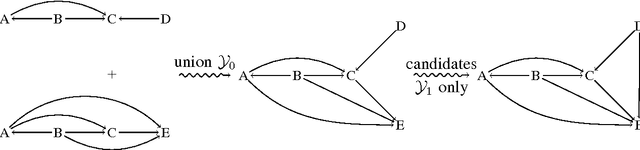
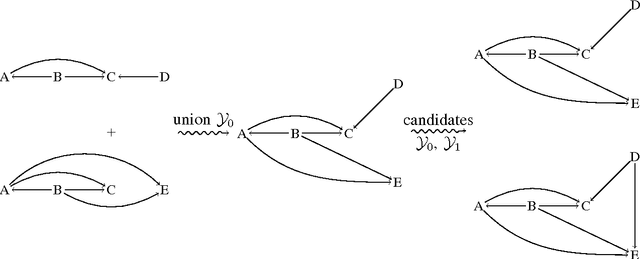
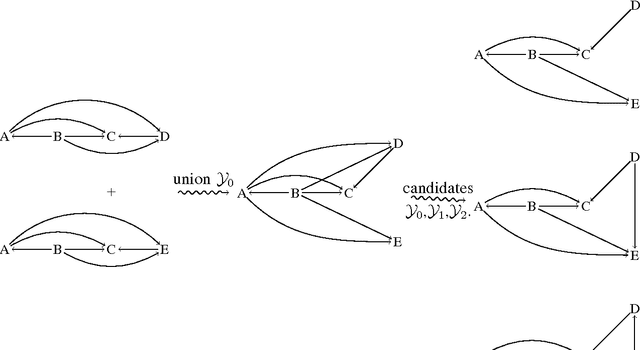
Frequent episode discovery is a popular framework for pattern discovery in event streams. An episode is a partially ordered set of nodes with each node associated with an event type. Efficient (and separate) algorithms exist for episode discovery when the associated partial order is total (serial episode) and trivial (parallel episode). In this paper, we propose efficient algorithms for discovering frequent episodes with general partial orders. These algorithms can be easily specialized to discover serial or parallel episodes. Also, the algorithms are flexible enough to be specialized for mining in the space of certain interesting subclasses of partial orders. We point out that there is an inherent combinatorial explosion in frequent partial order mining and most importantly, frequency alone is not a sufficient measure of interestingness. We propose a new interestingness measure for general partial order episodes and a discovery method based on this measure, for filtering out uninteresting partial orders. Simulations demonstrate the effectiveness of our algorithms.