Measuring temporal effects of agent knowledge by date-controlled tool use

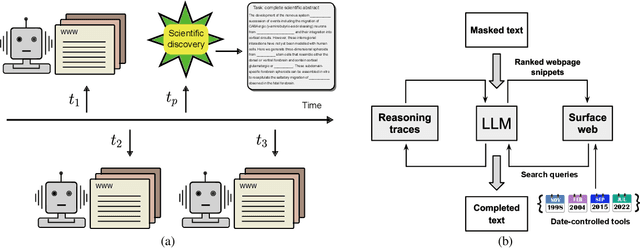
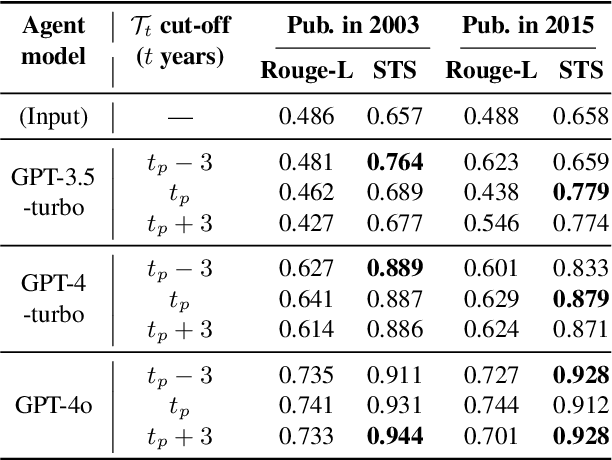
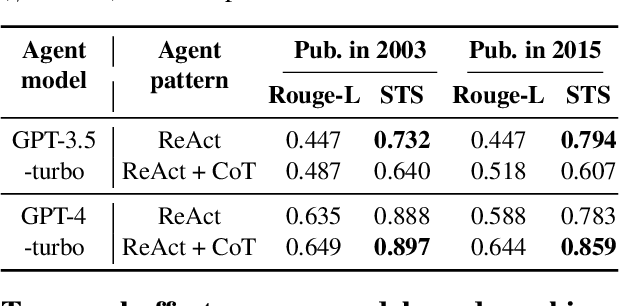
Temporal progression is an integral part of knowledge accumulation and update. Web search is frequently adopted as grounding for agent knowledge, yet its inappropriate configuration affects the quality of agent responses. Here, we construct a tool-based out-of-sample testing framework to measure the knowledge variability of large language model (LLM) agents from distinct date-controlled tools (DCTs). We demonstrate the temporal effects of an LLM agent as a writing assistant, which can use web search to help complete scientific publication abstracts. We show that temporal effects of the search engine translates into tool-dependent agent performance but can be alleviated with base model choice and explicit reasoning instructions such as chain-of-thought prompting. Our results indicate that agent evaluation should take a dynamical view and account for the temporal influence of tools and the updates of external resources.

Zero-shot sampling of adversarial entities in biomedical question answering

The increasing depth of parametric domain knowledge in large language models (LLMs) is fueling their rapid deployment in real-world applications. In high-stakes and knowledge-intensive tasks, understanding model vulnerabilities is essential for quantifying the trustworthiness of model predictions and regulating their use. The recent discovery of named entities as adversarial examples in natural language processing tasks raises questions about their potential guises in other settings. Here, we propose a powerscaled distance-weighted sampling scheme in embedding space to discover diverse adversarial entities as distractors. We demonstrate its advantage over random sampling in adversarial question answering on biomedical topics. Our approach enables the exploration of different regions on the attack surface, which reveals two regimes of adversarial entities that markedly differ in their characteristics. Moreover, we show that the attacks successfully manipulate token-wise Shapley value explanations, which become deceptive in the adversarial setting. Our investigations illustrate the brittleness of domain knowledge in LLMs and reveal a shortcoming of standard evaluations for high-capacity models.

From structure mining to unsupervised exploration of atomic octahedral networks

Networks of atom-centered coordination octahedra commonly occur in inorganic and hybrid solid-state materials. Characterizing their spatial arrangements and characteristics is crucial for relating structures to properties for many materials families. The traditional method using case-by-case inspection becomes prohibitive for discovering trends and similarities in large datasets. Here, we operationalize chemical intuition to automate the geometric parsing, quantification, and classification of coordination octahedral networks. We find axis-resolved tilting trends in ABO$_{3}$ perovskite polymorphs, which assist in detecting oxidation state changes. Moreover, we develop a scale-invariant encoding scheme to represent these networks, which, combined with human-assisted unsupervised machine learning, allows us to taxonomize the inorganic framework polytypes in hybrid iodoplumbates (A$_x$Pb$_y$I$_z$). Consequently, we uncover a violation of Pauling's third rule and the design principles underpinning their topological diversity. Our results offer a glimpse into the vast design space of atomic octahedral networks and inform high-throughput, targeted screening of specific structure types.