UniSearch: Rethinking Search System with a Unified Generative Architecture

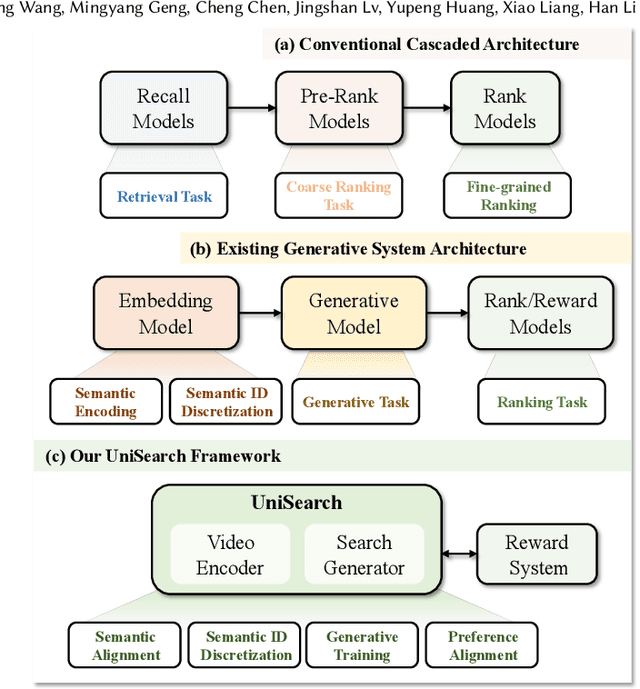
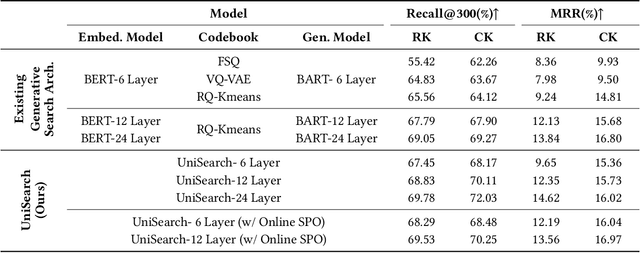
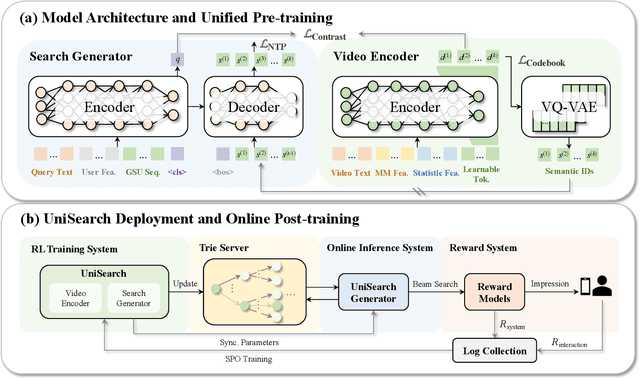
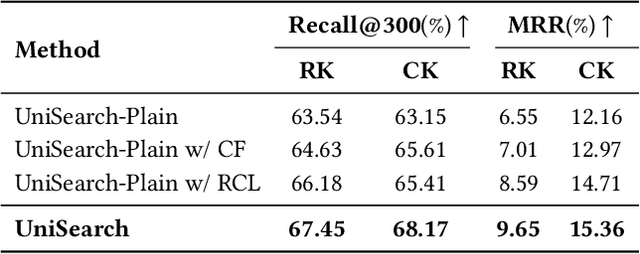
Modern search systems play a crucial role in facilitating information acquisition. Traditional search engines typically rely on a cascaded architecture, where results are retrieved through recall, pre-ranking, and ranking stages. The complexity of designing and maintaining multiple modules makes it difficult to achieve holistic performance gains. Recent advances in generative recommendation have motivated the exploration of unified generative search as an alternative. However, existing approaches are not genuinely end-to-end: they typically train an item encoder to tokenize candidates first and then optimize a generator separately, leading to objective inconsistency and limited generalization. To address these limitations, we propose UniSearch, a unified generative search framework for Kuaishou Search. UniSearch replaces the cascaded pipeline with an end-to-end architecture that integrates a Search Generator and a Video Encoder. The Generator produces semantic identifiers of relevant items given a user query, while the Video Encoder learns latent item embeddings and provides their tokenized representations. A unified training framework jointly optimizes both components, enabling mutual enhancement and improving representation quality and generation accuracy. Furthermore, we introduce Search Preference Optimization (SPO), which leverages a reward model and real user feedback to better align generation with user preferences. Extensive experiments on industrial-scale datasets, together with online A/B testing in both short-video and live search scenarios, demonstrate the strong effectiveness and deployment potential of UniSearch. Notably, its deployment in live search yields the largest single-experiment improvement in recent years of our product's history, highlighting its practical value for real-world applications.

Machine-Created Universal Language for Cross-lingual Transfer

There are two types of approaches to solving cross-lingual transfer: multilingual pre-training implicitly aligns the hidden representations of different languages, while the translate-test explicitly translates different languages to an intermediate language, such as English. Translate-test has better interpretability compared to multilingual pre-training. However, the translate-test has lower performance than multilingual pre-training(Conneau and Lample, 2019; Conneau et al, 2020) and can't solve word-level tasks because translation rearranges the word order. Therefore, we propose a new Machine-created Universal Language (MUL) as a new intermediate language. MUL consists of a set of discrete symbols as universal vocabulary and NL-MUL translator for translating from multiple natural languages to MUL. MUL unifies common concepts from different languages into the same universal word for better cross-language transfer. And MUL preserves the language-specific words as well as word order, so the model can be easily applied to word-level tasks. Our experiments show that translating into MUL achieves better performance compared to multilingual pre-training, and our analyses show that MUL has good interpretability.

Sparse Double Descent: Where Network Pruning Aggravates Overfitting

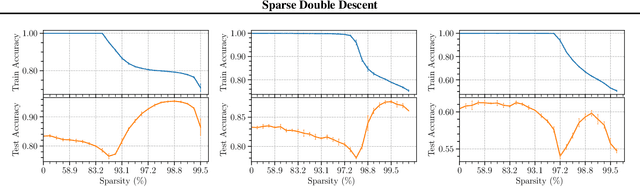
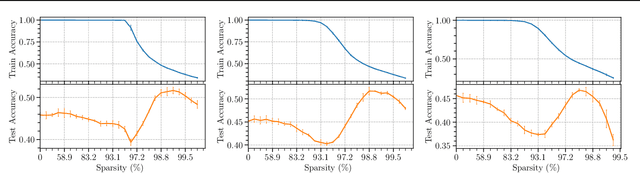
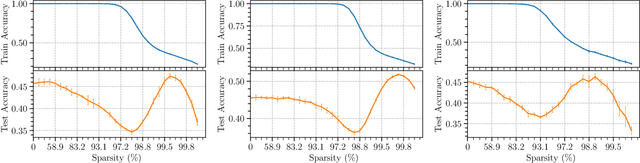
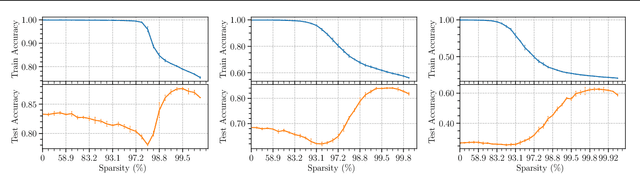
People usually believe that network pruning not only reduces the computational cost of deep networks, but also prevents overfitting by decreasing model capacity. However, our work surprisingly discovers that network pruning sometimes even aggravates overfitting. We report an unexpected sparse double descent phenomenon that, as we increase model sparsity via network pruning, test performance first gets worse (due to overfitting), then gets better (due to relieved overfitting), and gets worse at last (due to forgetting useful information). While recent studies focused on the deep double descent with respect to model overparameterization, they failed to recognize that sparsity may also cause double descent. In this paper, we have three main contributions. First, we report the novel sparse double descent phenomenon through extensive experiments. Second, for this phenomenon, we propose a novel learning distance interpretation that the curve of $\ell_{2}$ learning distance of sparse models (from initialized parameters to final parameters) may correlate with the sparse double descent curve well and reflect generalization better than minima flatness. Third, in the context of sparse double descent, a winning ticket in the lottery ticket hypothesis surprisingly may not always win.