Universality of Benign Overfitting in Binary Linear Classification

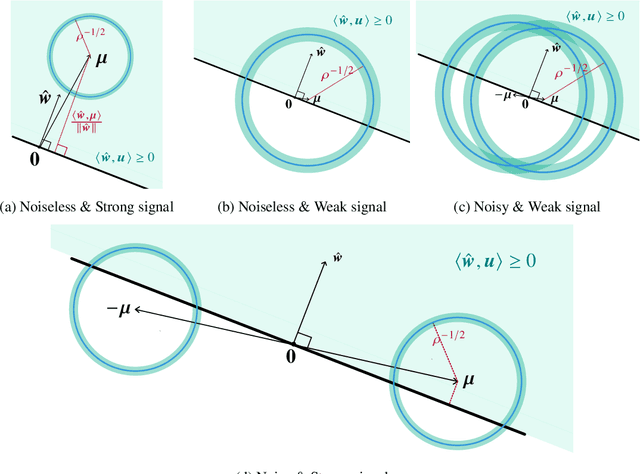
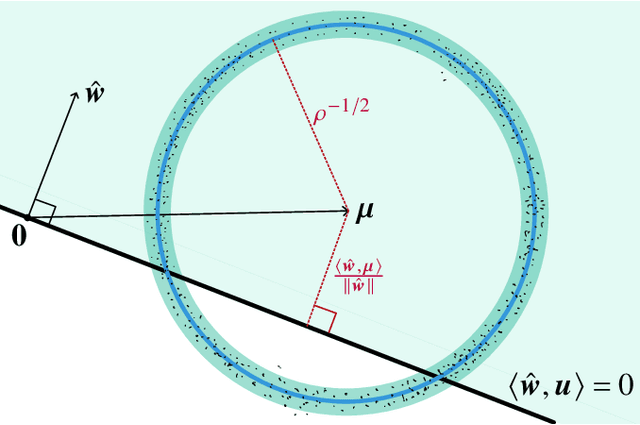
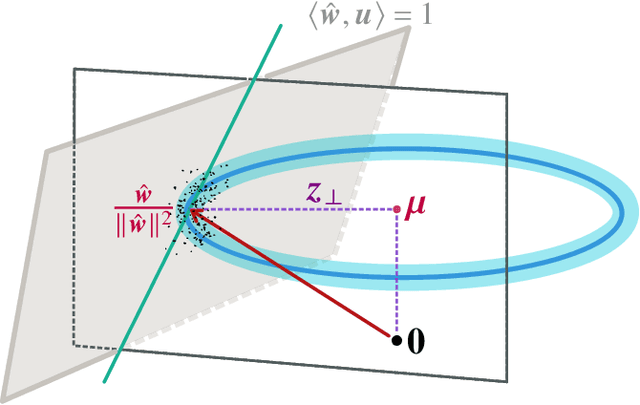
The practical success of deep learning has led to the discovery of several surprising phenomena. One of these phenomena, that has spurred intense theoretical research, is ``benign overfitting'': deep neural networks seem to generalize well in the over-parametrized regime even though the networks show a perfect fit to noisy training data. It is now known that benign overfitting also occurs in various classical statistical models. For linear maximum margin classifiers, benign overfitting has been established theoretically in a class of mixture models with very strong assumptions on the covariate distribution. However, even in this simple setting, many questions remain open. For instance, most of the existing literature focuses on the noiseless case where all true class labels are observed without errors, whereas the more interesting noisy case remains poorly understood. We provide a comprehensive study of benign overfitting for linear maximum margin classifiers. We discover a phase transition in test error bounds for the noisy model which was previously unknown and provide some geometric intuition behind it. We further considerably relax the required covariate assumptions in both, the noisy and noiseless case. Our results demonstrate that benign overfitting of maximum margin classifiers holds in a much wider range of scenarios than was previously known and provide new insights into the underlying mechanisms.

Entropic covariance models

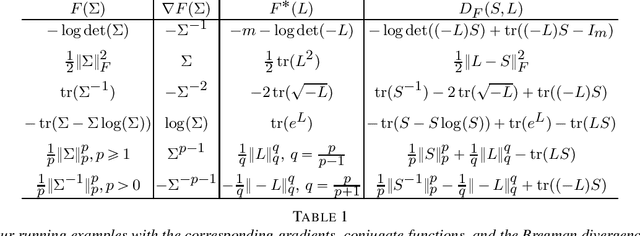
In covariance matrix estimation, one of the challenges lies in finding a suitable model and an efficient estimation method. Two commonly used approaches in the literature involve imposing linear restrictions on the covariance matrix or its inverse. Another approach considers linear restrictions on the matrix logarithm of the covariance matrix. In this paper, we present a general framework for linear restrictions on different transformations of the covariance matrix, including the mentioned examples. Our proposed estimation method solves a convex problem and yields an M-estimator, allowing for relatively straightforward asymptotic and finite sample analysis. After developing the general theory, we focus on modelling correlation matrices and on sparsity. Our geometric insights allow to extend various recent results in covariance matrix modelling. This includes providing unrestricted parametrizations of the space of correlation matrices, which is alternative to a recent result utilizing the matrix logarithm.

Robust estimation of tree structured models

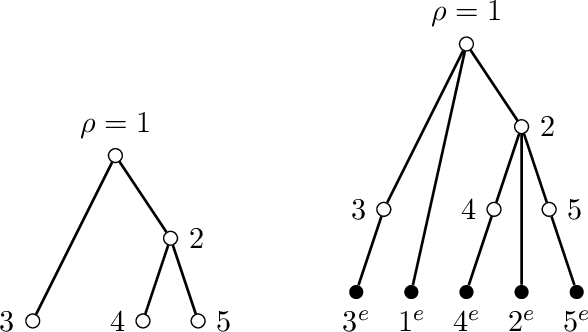
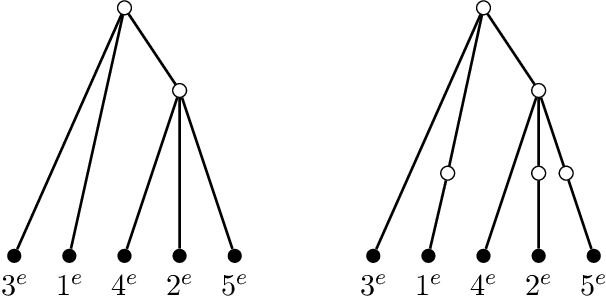
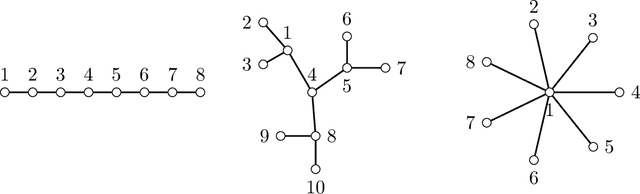
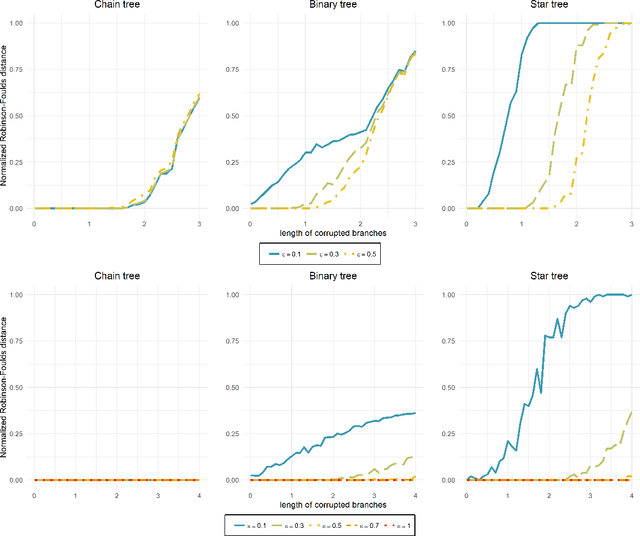
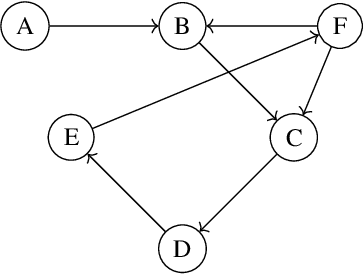
Consider the problem of learning undirected graphical models on trees from corrupted data. Recently Katiyar et al. showed that it is possible to recover trees from noisy binary data up to a small equivalence class of possible trees. Their other paper on the Gaussian case follows a similar pattern. By framing this as a special phylogenetic recovery problem we largely generalize these two settings. Using the framework of linear latent tree models we discuss tree identifiability for binary data under a continuous corruption model. For the Ising and the Gaussian tree model we also provide a characterisation of when the Chow-Liu algorithm consistently learns the underlying tree from the noisy data.

Structure learning in graphical models by covariance queries

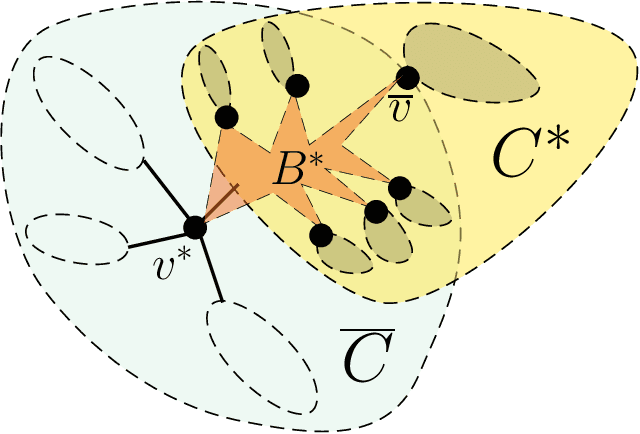
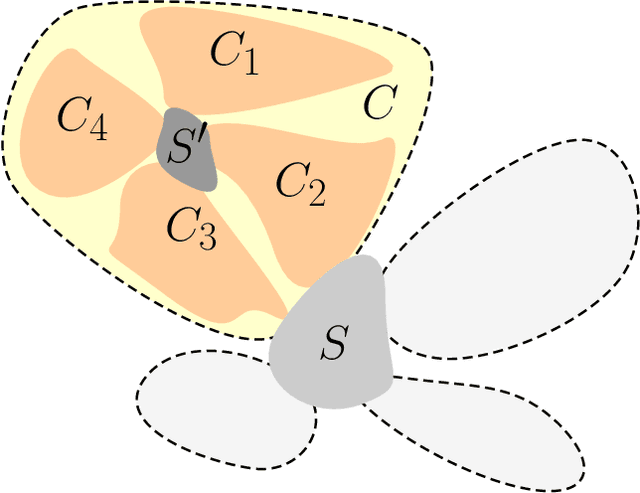
We study the problem of recovering the structure underlying large Gaussian graphical models. In high-dimensional problems it is often too costly to store the entire sample covariance matrix. We propose a new input model in which one can query single entries of the sample covariance matrix. We present computationally efficient algorithms for structure recovery in Gaussian graphical models with low query and computational complexity. Our algorithms work in a regime of tree-like graphs and, more generally, for graphs of small treewidth. Our results demonstrate that for large classes of graphs, the structure of the corresponding Gaussian graphical models can be determined much faster than even computing the empirical covariance matrix.

Latent tree models

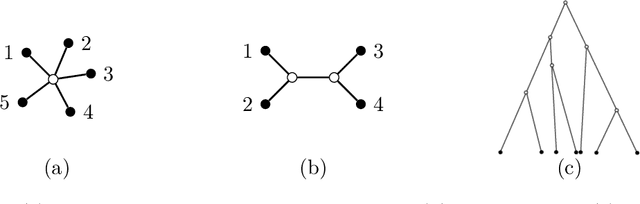
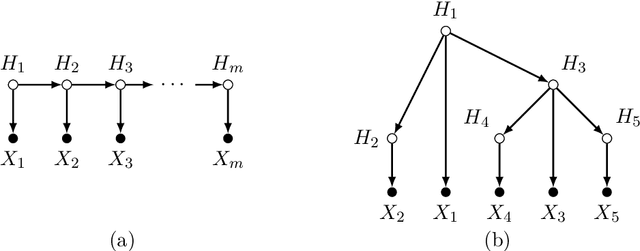
Latent tree models are graphical models defined on trees, in which only a subset of variables is observed. They were first discussed by Judea Pearl as tree-decomposable distributions to generalise star-decomposable distributions such as the latent class model. Latent tree models, or their submodels, are widely used in: phylogenetic analysis, network tomography, computer vision, causal modeling, and data clustering. They also contain other well-known classes of models like hidden Markov models, Brownian motion tree model, the Ising model on a tree, and many popular models used in phylogenetics. This article offers a concise introduction to the theory of latent tree models. We emphasise the role of tree metrics in the structural description of this model class, in designing learning algorithms, and in understanding fundamental limits of what and when can be learned.

Marginal likelihood and model selection for Gaussian latent tree and forest models

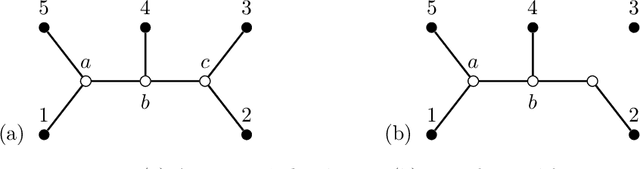
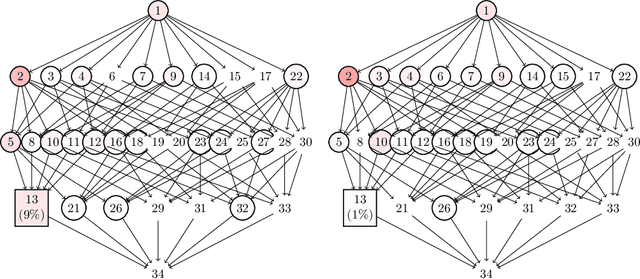
Gaussian latent tree models, or more generally, Gaussian latent forest models have Fisher-information matrices that become singular along interesting submodels, namely, models that correspond to subforests. For these singularities, we compute the real log-canonical thresholds (also known as stochastic complexities or learning coefficients) that quantify the large-sample behavior of the marginal likelihood in Bayesian inference. This provides the information needed for a recently introduced generalization of the Bayesian information criterion. Our mathematical developments treat the general setting of Laplace integrals whose phase functions are sums of squared differences between monomials and constants. We clarify how in this case real log-canonical thresholds can be computed using polyhedral geometry, and we show how to apply the general theory to the Laplace integrals associated with Gaussian latent tree and forest models. In simulations and a data example, we demonstrate how the mathematical knowledge can be applied in model selection.