Robust estimation of tree structured models
Paper and Code
Feb 10, 2021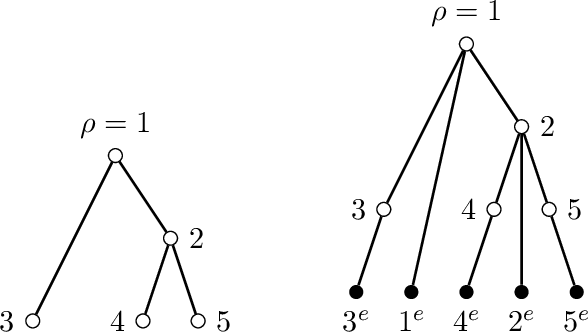
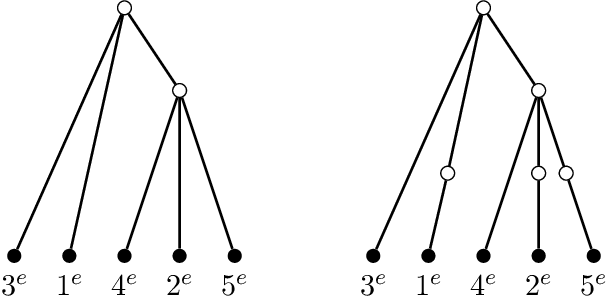
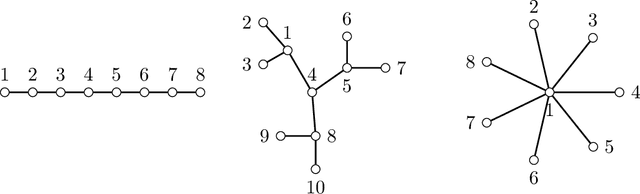
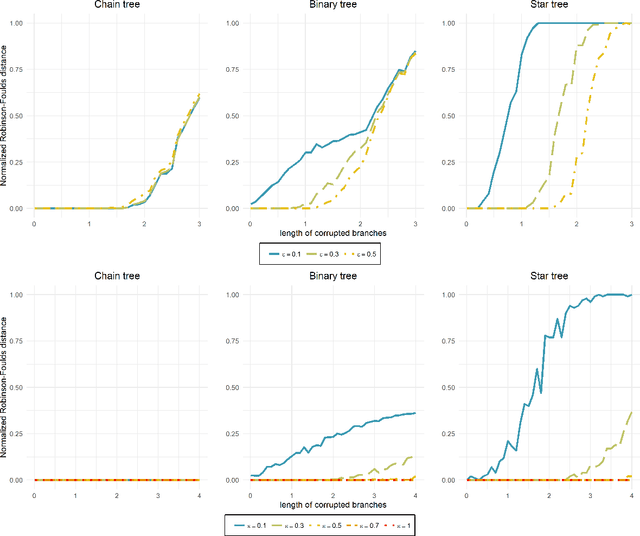
Consider the problem of learning undirected graphical models on trees from corrupted data. Recently Katiyar et al. showed that it is possible to recover trees from noisy binary data up to a small equivalence class of possible trees. Their other paper on the Gaussian case follows a similar pattern. By framing this as a special phylogenetic recovery problem we largely generalize these two settings. Using the framework of linear latent tree models we discuss tree identifiability for binary data under a continuous corruption model. For the Ising and the Gaussian tree model we also provide a characterisation of when the Chow-Liu algorithm consistently learns the underlying tree from the noisy data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge