Robust estimation of tree structured models

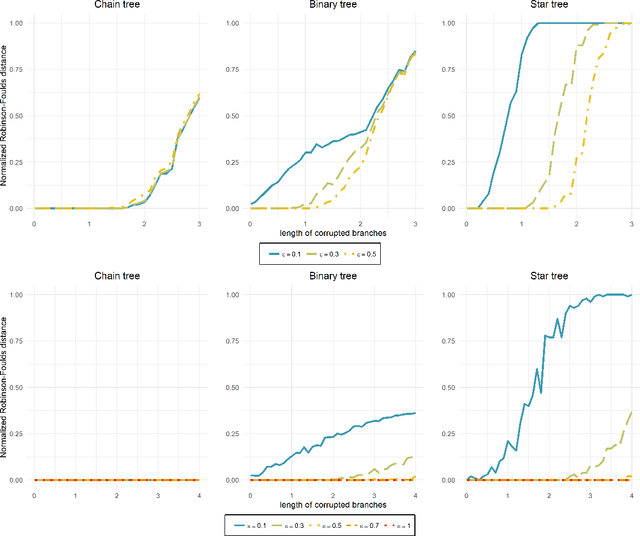
Consider the problem of learning undirected graphical models on trees from corrupted data. Recently Katiyar et al. showed that it is possible to recover trees from noisy binary data up to a small equivalence class of possible trees. Their other paper on the Gaussian case follows a similar pattern. By framing this as a special phylogenetic recovery problem we largely generalize these two settings. Using the framework of linear latent tree models we discuss tree identifiability for binary data under a continuous corruption model. For the Ising and the Gaussian tree model we also provide a characterisation of when the Chow-Liu algorithm consistently learns the underlying tree from the noisy data.

A New Spectral Method for Latent Variable Models

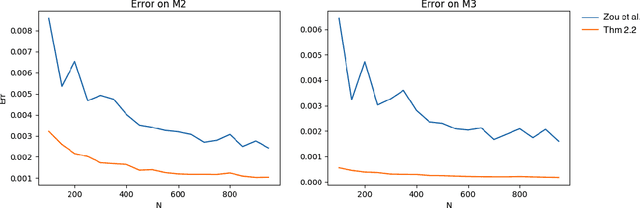
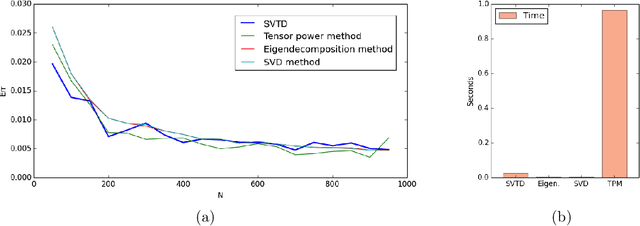
This paper presents an algorithm for the unsupervised learning of latent variable models from unlabeled sets of data. We base our technique on spectral decomposition, providing a technique that proves to be robust both in theory and in practice. We also describe how to use this algorithm to learn the parameters of two well known text mining models: single topic model and Latent Dirichlet Allocation, providing in both cases an efficient technique to retrieve the parameters to feed the algorithm. We compare the results of our algorithm with those of existing algorithms on synthetic data, and we provide examples of applications to real world text corpora for both single topic model and LDA, obtaining meaningful results.