Addressing materials' microstructure diversity using transfer learning

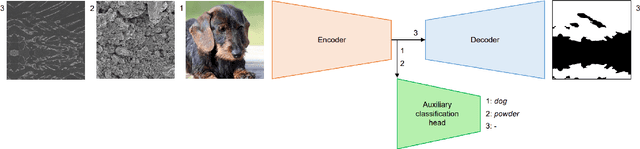
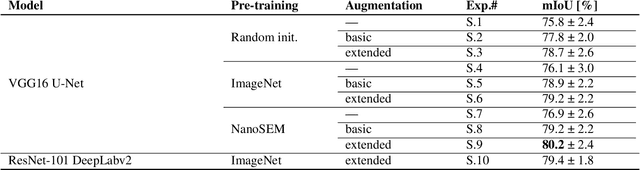
Materials' microstructures are signatures of their alloying composition and processing history. Therefore, microstructures exist in a wide variety. As materials become increasingly complex to comply with engineering demands, advanced computer vision (CV) approaches such as deep learning (DL) inevitably gain relevance for quantifying microstrucutures' constituents from micrographs. While DL can outperform classical CV techniques for many tasks, shortcomings are poor data efficiency and generalizability across datasets. This is inherently in conflict with the expense associated with annotating materials data through experts and extensive materials diversity. To tackle poor domain generalizability and the lack of labeled data simultaneously, we propose to apply a sub-class of transfer learning methods called unsupervised domain adaptation (UDA). These algorithms address the task of finding domain-invariant features when supplied with annotated source data and unannotated target data, such that performance on the latter distribution is optimized despite the absence of annotations. Exemplarily, this study is conducted on a lath-shaped bainite segmentation task in complex phase steel micrographs. Here, the domains to bridge are selected to be different metallographic specimen preparations (surface etchings) and distinct imaging modalities. We show that a state-of-the-art UDA approach surpasses the na\"ive application of source domain trained models on the target domain (generalization baseline) to a large extent. This holds true independent of the domain shift, despite using little data, and even when the baseline models were pre-trained or employed data augmentation. Through UDA, mIoU was improved over generalization baselines from 82.2%, 61.0%, 49.7% to 84.7%, 67.3%, 73.3% on three target datasets, respectively. This underlines this techniques' potential to cope with materials variance.

Bayesian Convolutional Neural Networks as probabilistic surrogates for the fast prediction of stress fields in structures with microscale features

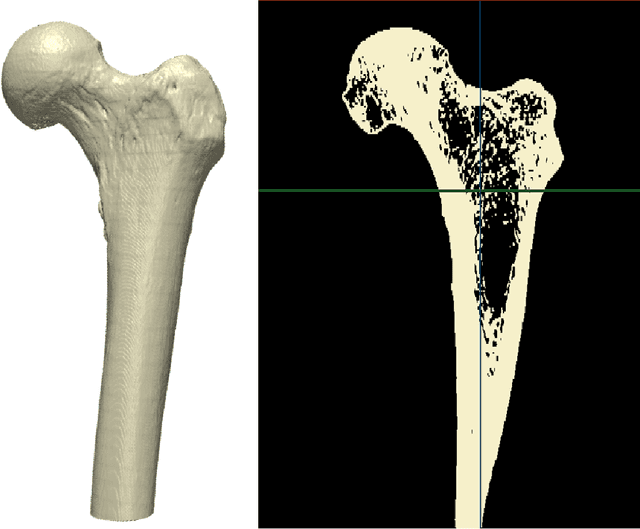
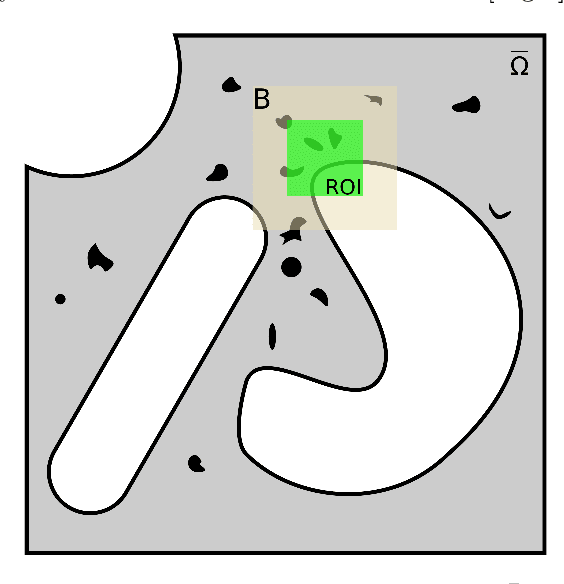
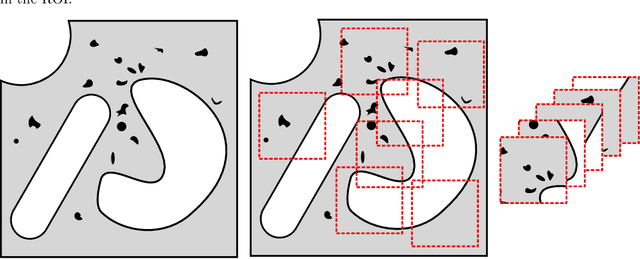
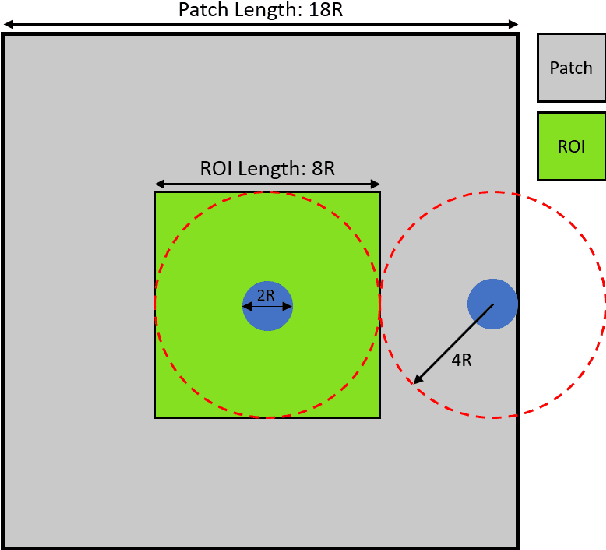
Finite Element Analysis (FEA) for stress prediction in structures with microstructural features is computationally expensive since those features are much smaller than the other geometric features of the structure. The accurate prediction of the additional stress generated by such microstructural features therefore requires a very fine FE mesh. Omitting or averaging the effect of the microstructural features from FEA models is standard practice, resulting in faster calculations of global stress fields, which, assuming some degree of scale separability, may then be complemented by local defect analyses. The purpose of this work is to train an Encoder-Decoder Convolutional Neural Networks (CNN) to automatically add local fine-scale stress corrections to coarse stress predictions around defects. We wish to understand to what extent such a framework may provide reliable stress predictions inside and outside the training set, i.e. for unseen coarse scale geometries and stress distributions and/or unseen defect geometries. Ultimately, we aim to develop efficient offline data generation and online data acquisition methods to maximise the domain of validity of the CNN predictions. To achieve these ambitious goals, we will deploy a Bayesian approach providing not point estimates, but credible intervals of the fine-scale stress field, as a means to evaluate the uncertainty of the predictions. The uncertainty quantified by the network will automatically encompass the lack of knowledge due to unseen macro and micro features, and the lack of knowledge due to the potential lack of scale separability. This uncertainty will be used in a Selective Learning framework to reduce the data requirements of the network. In this work we will investigate stress prediction in 2D composite structures with randomly distributed circular pores.