Bayesian Convolutional Neural Networks as probabilistic surrogates for the fast prediction of stress fields in structures with microscale features
Paper and Code
Dec 17, 2020
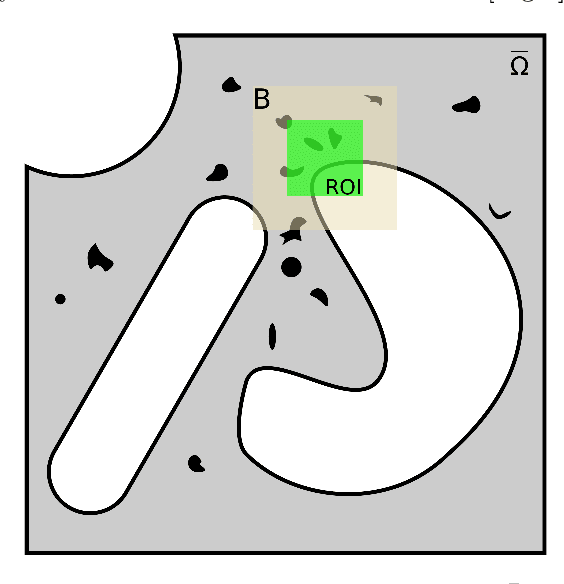
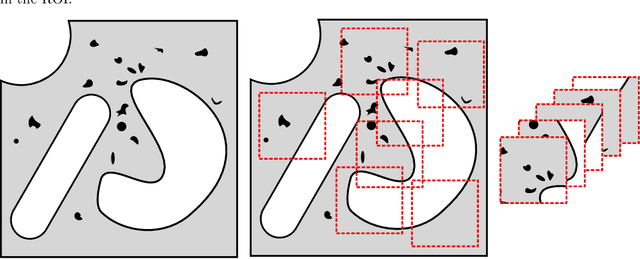
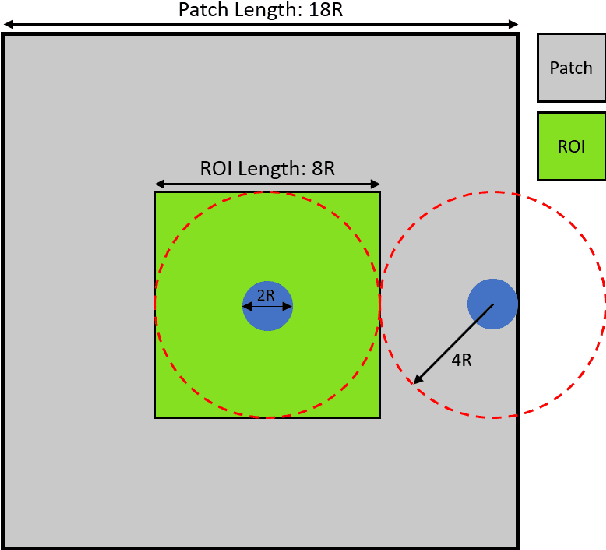
Finite Element Analysis (FEA) for stress prediction in structures with microstructural features is computationally expensive since those features are much smaller than the other geometric features of the structure. The accurate prediction of the additional stress generated by such microstructural features therefore requires a very fine FE mesh. Omitting or averaging the effect of the microstructural features from FEA models is standard practice, resulting in faster calculations of global stress fields, which, assuming some degree of scale separability, may then be complemented by local defect analyses. The purpose of this work is to train an Encoder-Decoder Convolutional Neural Networks (CNN) to automatically add local fine-scale stress corrections to coarse stress predictions around defects. We wish to understand to what extent such a framework may provide reliable stress predictions inside and outside the training set, i.e. for unseen coarse scale geometries and stress distributions and/or unseen defect geometries. Ultimately, we aim to develop efficient offline data generation and online data acquisition methods to maximise the domain of validity of the CNN predictions. To achieve these ambitious goals, we will deploy a Bayesian approach providing not point estimates, but credible intervals of the fine-scale stress field, as a means to evaluate the uncertainty of the predictions. The uncertainty quantified by the network will automatically encompass the lack of knowledge due to unseen macro and micro features, and the lack of knowledge due to the potential lack of scale separability. This uncertainty will be used in a Selective Learning framework to reduce the data requirements of the network. In this work we will investigate stress prediction in 2D composite structures with randomly distributed circular pores.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge