LD-EnSF: Synergizing Latent Dynamics with Ensemble Score Filters for Fast Data Assimilation with Sparse Observations

Data assimilation techniques are crucial for correcting the trajectory when modeling complex physical systems. A recently developed data assimilation method, Latent Ensemble Score Filter (Latent-EnSF), has shown great promise in addressing the key limitation of EnSF for highly sparse observations in high-dimensional and nonlinear data assimilation problems. It performs data assimilation in a latent space for encoded states and observations in every assimilation step, and requires costly full dynamics to be evolved in the original space. In this paper, we introduce Latent Dynamics EnSF (LD-EnSF), a novel methodology that completely avoids the full dynamics evolution and significantly accelerates the data assimilation process, which is especially valuable for complex dynamical problems that require fast data assimilation in real time. To accomplish this, we introduce a novel variant of Latent Dynamics Networks (LDNets) to effectively capture and preserve the system's dynamics within a very low-dimensional latent space. Additionally, we propose a new method for encoding sparse observations into the latent space using Long Short-Term Memory (LSTM) networks, which leverage not only the current step's observations, as in Latent-EnSF, but also all previous steps, thereby improving the accuracy and robustness of the observation encoding. We demonstrate the robustness, accuracy, and efficiency of the proposed method for two challenging dynamical systems with highly sparse (in both space and time) and noisy observations.

Latent-EnSF: A Latent Ensemble Score Filter for High-Dimensional Data Assimilation with Sparse Observation Data

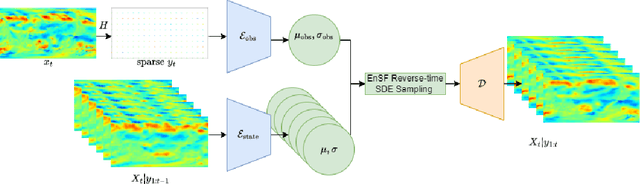
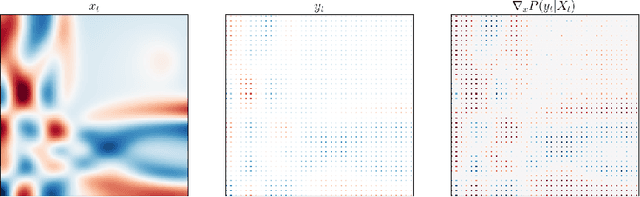
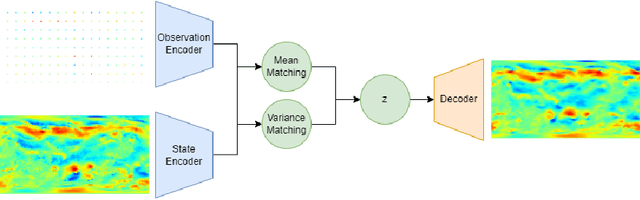
Accurate modeling and prediction of complex physical systems often rely on data assimilation techniques to correct errors inherent in model simulations. Traditional methods like the Ensemble Kalman Filter (EnKF) and its variants as well as the recently developed Ensemble Score Filters (EnSF) face significant challenges when dealing with high-dimensional and nonlinear Bayesian filtering problems with sparse observations, which are ubiquitous in real-world applications. In this paper, we propose a novel data assimilation method, Latent-EnSF, which leverages EnSF with efficient and consistent latent representations of the full states and sparse observations to address the joint challenges of high dimensionlity in states and high sparsity in observations for nonlinear Bayesian filtering. We introduce a coupled Variational Autoencoder (VAE) with two encoders to encode the full states and sparse observations in a consistent way guaranteed by a latent distribution matching and regularization as well as a consistent state reconstruction. With comparison to several methods, we demonstrate the higher accuracy, faster convergence, and higher efficiency of Latent-EnSF for two challenging applications with complex models in shallow water wave propagation and medium-range weather forecasting, for highly sparse observations in both space and time.

ECGBERT: Understanding Hidden Language of ECGs with Self-Supervised Representation Learning

In the medical field, current ECG signal analysis approaches rely on supervised deep neural networks trained for specific tasks that require substantial amounts of labeled data. However, our paper introduces ECGBERT, a self-supervised representation learning approach that unlocks the underlying language of ECGs. By unsupervised pre-training of the model, we mitigate challenges posed by the lack of well-labeled and curated medical data. ECGBERT, inspired by advances in the area of natural language processing and large language models, can be fine-tuned with minimal additional layers for various ECG-based problems. Through four tasks, including Atrial Fibrillation arrhythmia detection, heartbeat classification, sleep apnea detection, and user authentication, we demonstrate ECGBERT's potential to achieve state-of-the-art results on a wide variety of tasks.

Energy Flows: Towards Determinant-Free Training of Normalizing Flows

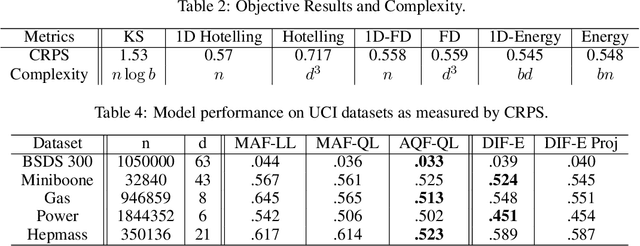
Normalizing flows are a popular approach for constructing probabilistic and generative models. However, maximum likelihood training of flows is challenging due to the need to calculate computationally expensive determinants of Jacobians. This paper takes steps towards addressing this challenge by introducing an approach for determinant-free training of flows inspired by two-sample testing. Central to our framework is the energy objective, a multidimensional extension of proper scoring rules that admits efficient estimators based on random projections and that outperforms a range of alternative two-sample objectives that can be derived in our framework. Crucially, the energy objective and its alternatives do not require calculating determinants and therefore support general flow architectures that are not well-suited to maximum likelihood training (e.g., densely connected networks). We empirically demonstrate that energy flows achieve competitive generative modeling performance while maintaining fast generation and posterior inference.

Autoregressive Quantile Flows for Predictive Uncertainty Estimation

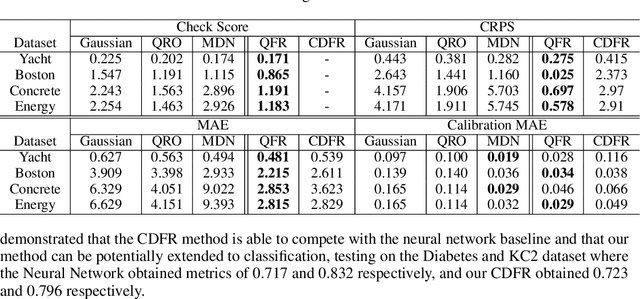
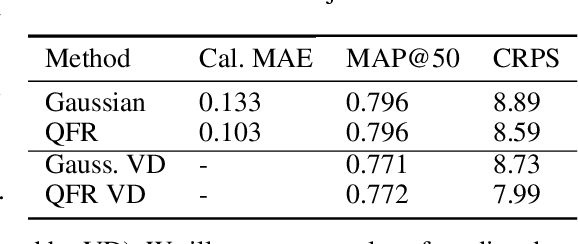
Numerous applications of machine learning involve predicting flexible probability distributions over model outputs. We propose Autoregressive Quantile Flows, a flexible class of probabilistic models over high-dimensional variables that can be used to accurately capture predictive aleatoric uncertainties. These models are instances of autoregressive flows trained using a novel objective based on proper scoring rules, which simplifies the calculation of computationally expensive determinants of Jacobians during training and supports new types of neural architectures. We demonstrate that these models can be used to parameterize predictive conditional distributions and improve the quality of probabilistic predictions on time series forecasting and object detection.