Latent-EnSF: A Latent Ensemble Score Filter for High-Dimensional Data Assimilation with Sparse Observation Data
Paper and Code
Aug 29, 2024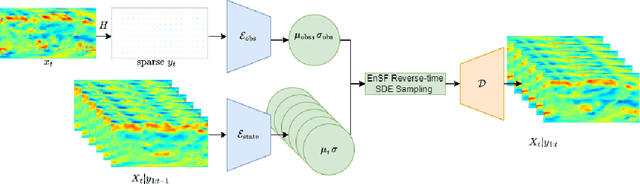

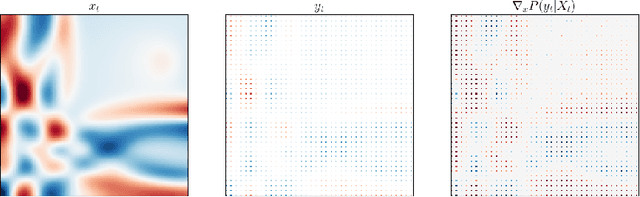
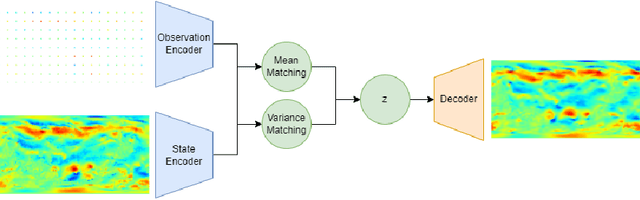
Accurate modeling and prediction of complex physical systems often rely on data assimilation techniques to correct errors inherent in model simulations. Traditional methods like the Ensemble Kalman Filter (EnKF) and its variants as well as the recently developed Ensemble Score Filters (EnSF) face significant challenges when dealing with high-dimensional and nonlinear Bayesian filtering problems with sparse observations, which are ubiquitous in real-world applications. In this paper, we propose a novel data assimilation method, Latent-EnSF, which leverages EnSF with efficient and consistent latent representations of the full states and sparse observations to address the joint challenges of high dimensionlity in states and high sparsity in observations for nonlinear Bayesian filtering. We introduce a coupled Variational Autoencoder (VAE) with two encoders to encode the full states and sparse observations in a consistent way guaranteed by a latent distribution matching and regularization as well as a consistent state reconstruction. With comparison to several methods, we demonstrate the higher accuracy, faster convergence, and higher efficiency of Latent-EnSF for two challenging applications with complex models in shallow water wave propagation and medium-range weather forecasting, for highly sparse observations in both space and time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge