Energy Flows: Towards Determinant-Free Training of Normalizing Flows
Paper and Code
Jun 14, 2022


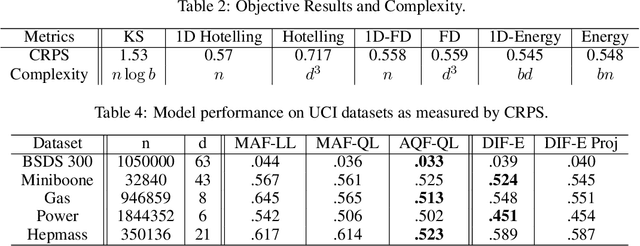
Normalizing flows are a popular approach for constructing probabilistic and generative models. However, maximum likelihood training of flows is challenging due to the need to calculate computationally expensive determinants of Jacobians. This paper takes steps towards addressing this challenge by introducing an approach for determinant-free training of flows inspired by two-sample testing. Central to our framework is the energy objective, a multidimensional extension of proper scoring rules that admits efficient estimators based on random projections and that outperforms a range of alternative two-sample objectives that can be derived in our framework. Crucially, the energy objective and its alternatives do not require calculating determinants and therefore support general flow architectures that are not well-suited to maximum likelihood training (e.g., densely connected networks). We empirically demonstrate that energy flows achieve competitive generative modeling performance while maintaining fast generation and posterior inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge