Allan Bishop
Autoregressive Quantile Flows for Predictive Uncertainty Estimation
Dec 09, 2021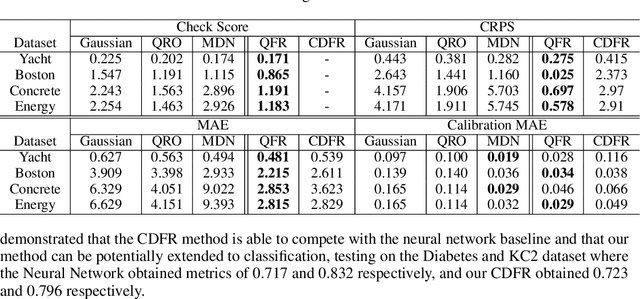


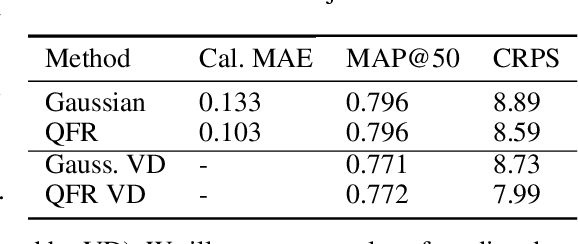
Abstract:Numerous applications of machine learning involve predicting flexible probability distributions over model outputs. We propose Autoregressive Quantile Flows, a flexible class of probabilistic models over high-dimensional variables that can be used to accurately capture predictive aleatoric uncertainties. These models are instances of autoregressive flows trained using a novel objective based on proper scoring rules, which simplifies the calculation of computationally expensive determinants of Jacobians during training and supports new types of neural architectures. We demonstrate that these models can be used to parameterize predictive conditional distributions and improve the quality of probabilistic predictions on time series forecasting and object detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge