Discovery and Recognition of Formula Concepts using Machine Learning

Citation-based Information Retrieval (IR) methods for scientific documents have proven effective for IR applications, such as Plagiarism Detection or Literature Recommender Systems in academic disciplines that use many references. In science, technology, engineering, and mathematics, researchers often employ mathematical concepts through formula notation to refer to prior knowledge. Our long-term goal is to generalize citation-based IR methods and apply this generalized method to both classical references and mathematical concepts. In this paper, we suggest how mathematical formulas could be cited and define a Formula Concept Retrieval task with two subtasks: Formula Concept Discovery (FCD) and Formula Concept Recognition (FCR). While FCD aims at the definition and exploration of a 'Formula Concept' that names bundled equivalent representations of a formula, FCR is designed to match a given formula to a prior assigned unique mathematical concept identifier. We present machine learning-based approaches to address the FCD and FCR tasks. We then evaluate these approaches on a standardized test collection (NTCIR arXiv dataset). Our FCD approach yields a precision of 68% for retrieving equivalent representations of frequent formulas and a recall of 72% for extracting the formula name from the surrounding text. FCD and FCR enable the citation of formulas within mathematical documents and facilitate semantic search and question answering as well as document similarity assessments for plagiarism detection or recommender systems.

Collaborative and AI-aided Exam Question Generation using Wikidata in Education

Since the COVID-19 outbreak, the use of digital learning or education platforms has significantly increased. Teachers now digitally distribute homework and provide exercise questions. In both cases, teachers need to continuously develop novel and individual questions. This process can be very time-consuming and should be facilitated and accelerated both through exchange with other teachers and by using Artificial Intelligence (AI) capabilities. To address this need, we propose a multilingual Wikimedia framework that allows for collaborative worldwide teacher knowledge engineering and subsequent AI-aided question generation, test, and correction. As a proof of concept, we present >>PhysWikiQuiz<<, a physics question generation and test engine. Our system (hosted by Wikimedia at https://physwikiquiz.wmflabs.org) retrieves physics knowledge from the open community-curated database Wikidata. It can generate questions in different variations and verify answer values and units using a Computer Algebra System (CAS). We evaluate the performance on a public benchmark dataset at each stage of the system workflow. For an average formula with three variables, the system can generate and correct up to 300 questions for individual students based on a single formula concept name as input by the teacher.

Mining Mathematical Documents for Question Answering via Unsupervised Formula Labeling

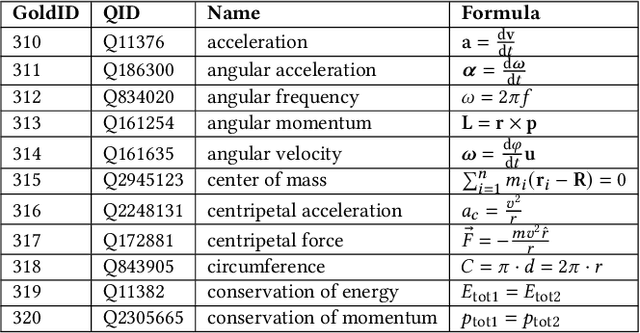
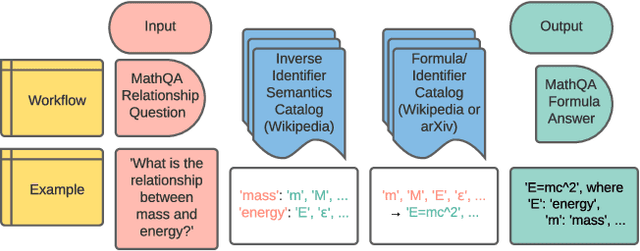
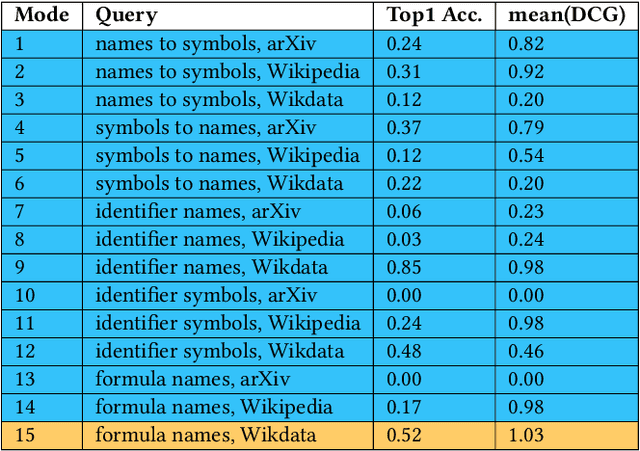
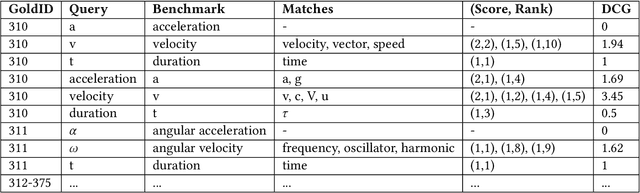
The increasing number of questions on Question Answering (QA) platforms like Math Stack Exchange (MSE) signifies a growing information need to answer math-related questions. However, there is currently very little research on approaches for an open data QA system that retrieves mathematical formulae using their concept names or querying formula identifier relationships from knowledge graphs. In this paper, we aim to bridge the gap by presenting data mining methods and benchmark results to employ Mathematical Entity Linking (MathEL) and Unsupervised Formula Labeling (UFL) for semantic formula search and mathematical question answering (MathQA) on the arXiv preprint repository, Wikipedia, and Wikidata, which is part of the Wikimedia ecosystem of free knowledge. Based on different types of information needs, we evaluate our system in 15 information need modes, assessing over 7,000 query results. Furthermore, we compare its performance to a commercial knowledge-base and calculation-engine (Wolfram Alpha) and search-engine (Google). The open source system is hosted by Wikimedia at https://mathqa.wmflabs.org. A demovideo is available at purl.org/mathqa.

Towards Explaining STEM Document Classification using Mathematical Entity Linking

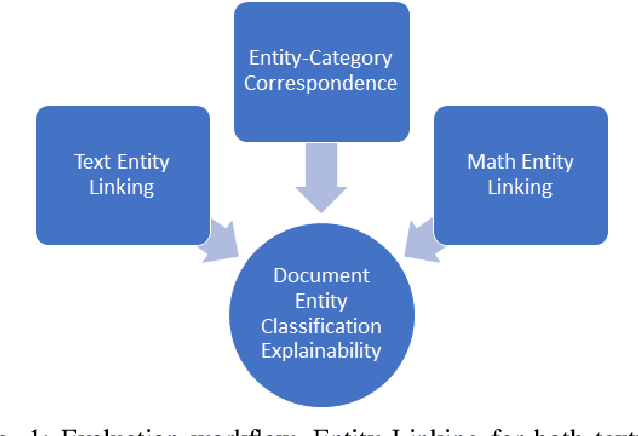
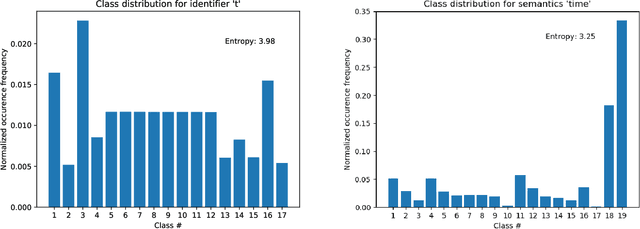
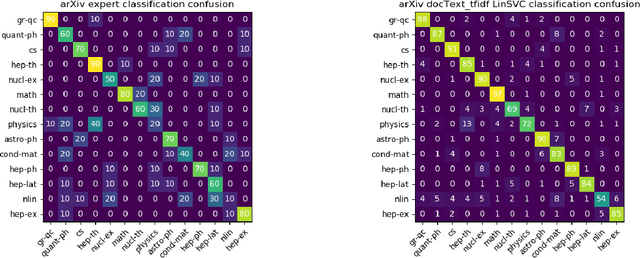
Document subject classification is essential for structuring (digital) libraries and allowing readers to search within a specific field. Currently, the classification is typically made by human domain experts. Semi-supervised Machine Learning algorithms can support them by exploiting the labeled data to predict subject classes for unclassified new documents. However, while humans partly do, machines mostly do not explain the reasons for their decisions. Recently, explainable AI research to address the problem of Machine Learning decisions being a black box has increasingly gained interest. Explainer models have already been applied to the classification of natural language texts, such as legal or medical documents. Documents from Science, Technology, Engineering, and Mathematics (STEM) disciplines are more difficult to analyze, since they contain both textual and mathematical formula content. In this paper, we present first advances towards STEM document classification explainability using classical and mathematical Entity Linking. We examine relationships between textual and mathematical subject classes and entities, mining a collection of documents from the arXiv preprint repository (NTCIR and zbMATH dataset). The results indicate that mathematical entities have the potential to provide high explainability as they are a crucial part of a STEM document.

AutoMSC: Automatic Assignment of Mathematics Subject Classification Labels

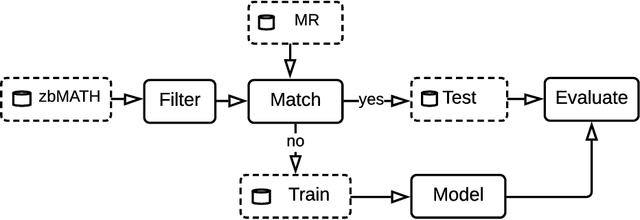
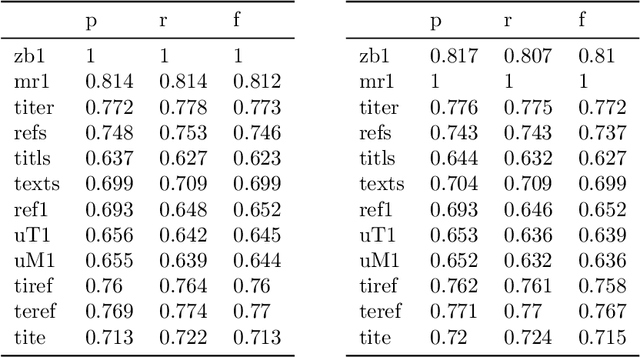
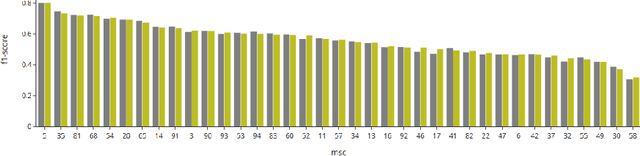
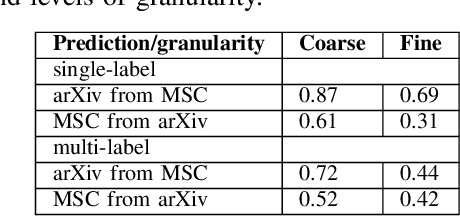
Authors of research papers in the fields of mathematics, and other math-heavy disciplines commonly employ the Mathematics Subject Classification (MSC) scheme to search for relevant literature. The MSC is a hierarchical alphanumerical classification scheme that allows librarians to specify one or multiple codes for publications. Digital Libraries in Mathematics, as well as reviewing services, such as zbMATH and Mathematical Reviews (MR) rely on these MSC labels in their workflows to organize the abstracting and reviewing process. Especially, the coarse-grained classification determines the subject editor who is responsible for the actual reviewing process. In this paper, we investigate the feasibility of automatically assigning a coarse-grained primary classification using the MSC scheme, by regarding the problem as a multi class classification machine learning task. We find that the our method achieves an (F_{1})-score of over 77%, which is remarkably close to the agreement of zbMATH and MR ((F_{1})-score of 81%). Moreover, we find that the method's confidence score allows for reducing the effort by 86\% compared to the manual coarse-grained classification effort while maintaining a precision of 81% for automatically classified articles.

Classification and Clustering of arXiv Documents, Sections, and Abstracts, Comparing Encodings of Natural and Mathematical Language

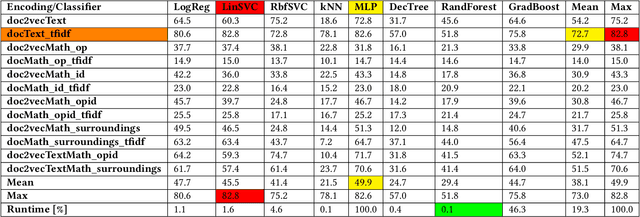
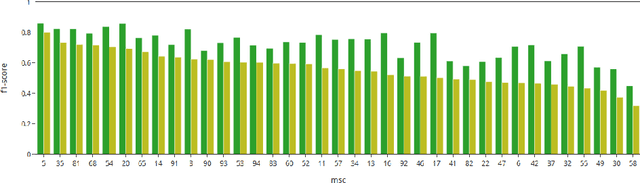
In this paper, we show how selecting and combining encodings of natural and mathematical language affect classification and clustering of documents with mathematical content. We demonstrate this by using sets of documents, sections, and abstracts from the arXiv preprint server that are labeled by their subject class (mathematics, computer science, physics, etc.) to compare different encodings of text and formulae and evaluate the performance and runtimes of selected classification and clustering algorithms. Our encodings achieve classification accuracies up to $82.8\%$ and cluster purities up to $69.4\%$ (number of clusters equals number of classes), and $99.9\%$ (unspecified number of clusters) respectively. We observe a relatively low correlation between text and math similarity, which indicates the independence of text and formulae and motivates treating them as separate features of a document. The classification and clustering can be employed, e.g., for document search and recommendation. Furthermore, we show that the computer outperforms a human expert when classifying documents. Finally, we evaluate and discuss multi-label classification and formula semantification.

Introducing MathQA -- A Math-Aware Question Answering System

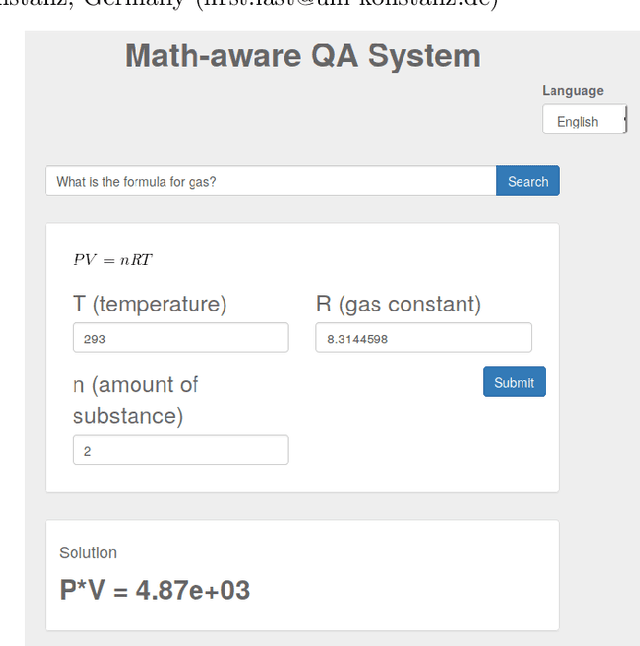
We present an open source math-aware Question Answering System based on Ask Platypus. Our system returns as a single mathematical formula for a natural language question in English or Hindi. This formulae originate from the knowledge-base Wikidata. We translate these formulae to computable data by integrating the calculation engine sympy into our system. This way, users can enter numeric values for the variables occurring in the formula. Moreover, the system loads numeric values for constants occurring in the formula from Wikidata. In a user study, our system outperformed a commercial computational mathematical knowledge engine by 13%. However, the performance of our system heavily depends on the size and quality of the formula data available in Wikidata. Since only a few items in Wikidata contained formulae when we started the project, we facilitated the import process by suggesting formula edits to Wikidata editors. With the simple heuristic that the first formula is significant for the article, 80% of the suggestions were correct.