Sparse outlier-robust PCA for multi-source data

Sparse and outlier-robust Principal Component Analysis (PCA) has been a very active field of research recently. Yet, most existing methods apply PCA to a single dataset whereas multi-source data-i.e. multiple related datasets requiring joint analysis-arise across many scientific areas. We introduce a novel PCA methodology that simultaneously (i) selects important features, (ii) allows for the detection of global sparse patterns across multiple data sources as well as local source-specific patterns, and (iii) is resistant to outliers. To this end, we develop a regularization problem with a penalty that accommodates global-local structured sparsity patterns, and where the ssMRCD estimator is used as plug-in to permit joint outlier-robust analysis across multiple data sources. We provide an efficient implementation of our proposal via the Alternating Direction Method of Multiplier and illustrate its practical advantages in simulation and in applications.

Efficient Computation of Sparse and Robust Maximum Association Estimators

Although robust statistical estimators are less affected by outlying observations, their computation is usually more challenging. This is particularly the case in high-dimensional sparse settings. The availability of new optimization procedures, mainly developed in the computer science domain, offers new possibilities for the field of robust statistics. This paper investigates how such procedures can be used for robust sparse association estimators. The problem can be split into a robust estimation step followed by an optimization for the remaining decoupled, (bi-)convex problem. A combination of the augmented Lagrangian algorithm and adaptive gradient descent is implemented to also include suitable constraints for inducing sparsity. We provide results concerning the precision of the algorithm and show the advantages over existing algorithms in this context. High-dimensional empirical examples underline the usefulness of this procedure. Extensions to other robust sparse estimators are possible.

Improving Forecasts for Heterogeneous Time Series by "Averaging", with Application to Food Demand Forecast

A common forecasting setting in real world applications considers a set of possibly heterogeneous time series of the same domain. Due to different properties of each time series such as length, obtaining forecasts for each individual time series in a straight-forward way is challenging. This paper proposes a general framework utilizing a similarity measure in Dynamic Time Warping to find similar time series to build neighborhoods in a k-Nearest Neighbor fashion, and improve forecasts of possibly simple models by averaging. Several ways of performing the averaging are suggested, and theoretical arguments underline the usefulness of averaging for forecasting. Additionally, diagnostics tools are proposed allowing a deep understanding of the procedure.

Predictive change point detection for heterogeneous data

A change point detection (CPD) framework assisted by a predictive machine learning model called ''Predict and Compare'' is introduced and characterised in relation to other state-of-the-art online CPD routines which it outperforms in terms of false positive rate and out-of-control average run length. The method's focus is on improving standard methods from sequential analysis such as the CUSUM rule in terms of these quality measures. This is achieved by replacing typically used trend estimation functionals such as the running mean with more sophisticated predictive models (Predict step), and comparing their prognosis with actual data (Compare step). The two models used in the Predict step are the ARIMA model and the LSTM recursive neural network. However, the framework is formulated in general terms, so as to allow the use of other prediction or comparison methods than those tested here. The power of the method is demonstrated in a tribological case study in which change points separating the run-in, steady-state, and divergent wear phases are detected in the regime of very few false positives.

Multivariate outlier explanations using Shapley values and Mahalanobis distances

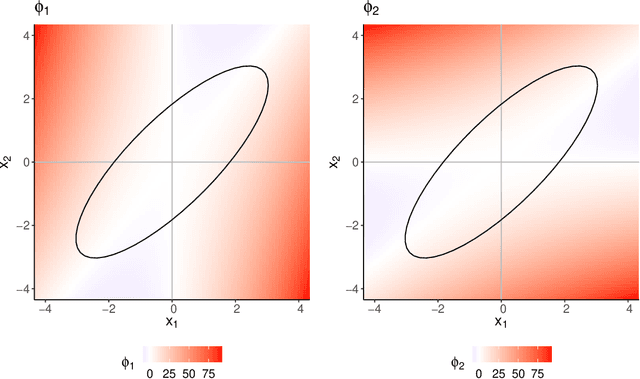
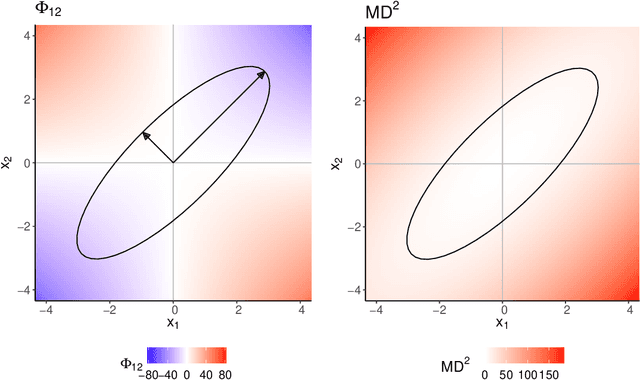
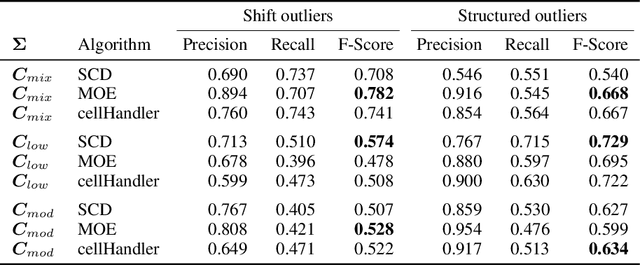
For the purpose of explaining multivariate outlyingness, it is shown that the squared Mahalanobis distance of an observation can be decomposed into outlyingness contributions originating from single variables. The decomposition is obtained using the Shapley value, a well-known concept from game theory that became popular in the context of Explainable AI. In addition to outlier explanation, this concept also relates to the recent formulation of cellwise outlyingness, where Shapley values can be employed to obtain variable contributions for outlying observations with respect to their "expected" position given the multivariate data structure. In combination with squared Mahalanobis distances, Shapley values can be calculated at a low numerical cost, making them even more attractive for outlier interpretation. Simulations and real-world data examples demonstrate the usefulness of these concepts.

Identifying the root cause of cable network problems with machine learning

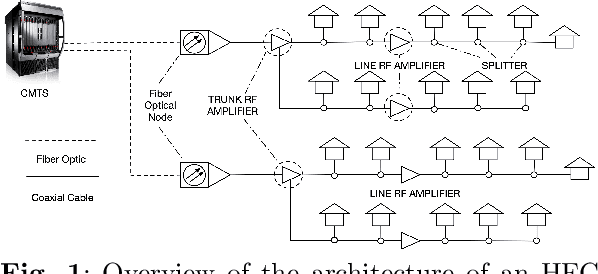
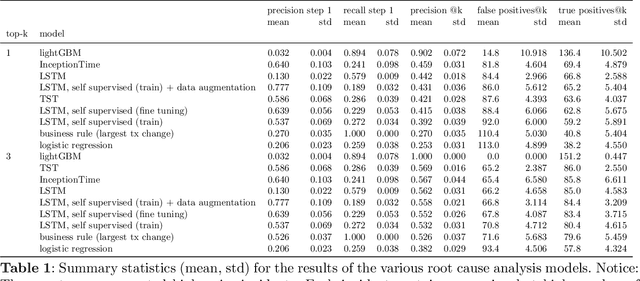
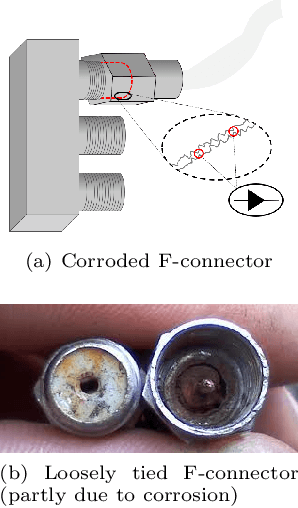
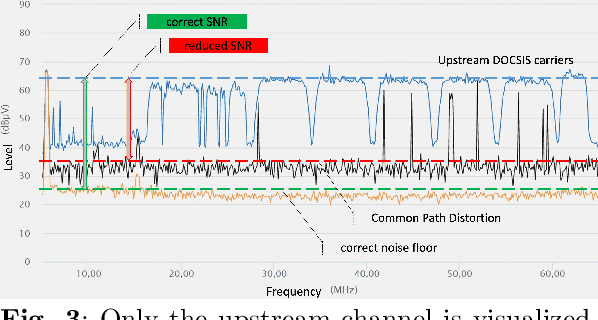
Good quality network connectivity is ever more important. For hybrid fiber coaxial (HFC) networks, searching for upstream high noise in the past was cumbersome and time-consuming. Even with machine learning due to the heterogeneity of the network and its topological structure, the task remains challenging. We present the automation of a simple business rule (largest change of a specific value) and compare its performance with state-of-the-art machine-learning methods and conclude that the precision@1 can be improved by 2.3 times. As it is best when a fault does not occur in the first place, we secondly evaluate multiple approaches to forecast network faults, which would allow performing predictive maintenance on the network.

Extending compositional data analysis from a graph signal processing perspective

Traditional methods for the analysis of compositional data consider the log-ratios between all different pairs of variables with equal weight, typically in the form of aggregated contributions. This is not meaningful in contexts where it is known that a relationship only exists between very specific variables (e.g.~for metabolomic pathways), while for other pairs a relationship does not exist. Modeling absence or presence of relationships is done in graph theory, where the vertices represent the variables, and the connections refer to relations. This paper links compositional data analysis with graph signal processing, and it extends the Aitchison geometry to a setting where only selected log-ratios can be considered. The presented framework retains the desirable properties of scale invariance and compositional coherence. An additional extension to include absolute information is readily made. Examples from bioinformatics and geochemistry underline the usefulness of thisapproach in comparison to standard methods for compositional data analysis.